Question

11．已知空间四边形ABCD中，E，F分别是AC，BD的中点，若AB=CD=4，EF=2，则EF与AB所成的角为（　　）

• A． 30°
• B． 45°
• C． 60°
• D． 90°

Answer 1

分析 取CD的中点G，连接FG，EG，又E为AC的中点．利用三角形的中位线定理可得，∠FEG即为异面直线EF与AB所成的角或其补角．同理可得FG=$\frac{1}{2}$BC=2，可得△EFG为等边三角形．进而得出．

解答 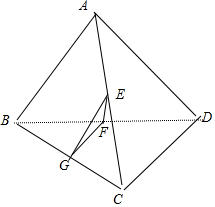解：如图所示，取CB的中点G，连接FG，EG，又E为AC的中点．∴$EG∥AB，EG=\frac{1}{2}AB=2$
∴∠FEG即为异面直线EF与AB所成的角或其补角．
∵F为BD的中点，同理可得FG=$\frac{1}{2}CD=2$BC．
∴EF=FG=EG．∴△EFG为等边三角形．
∴∠FEG=60°．即异面直线EF与AB所成的角为60°．
故选：C．

点评 本题考查了异面直线所成的夹角、三角形的中位线定理、等边三角形的定义及其性质，考查了推理能力和计算能力，考查了空间想象能力．