
分析 (Ⅰ)根据R1(An)和Rn(An)的定义,结合已知中A3=$\overline{110}$,可得答案;
(Ⅱ)列举出所有的3位排列,根据最佳排列的定义可得,最佳排列A3;
(Ⅲ)由 t(A5,R1(A5))=-1,可得|a1-a5|,|a2-a1|,|a3-a2|,|a4-a3|,|a5-a4|之中有2个0,3个1,而a5经过奇数次数码改变不能回到自身,所以不存在A5,使得t(A5,R1(A5))=-1.
解答 解:(Ⅰ)当A3=$\overline{110}$,R1(A3)=$\overline{011}$,
t(A3,R1(A3))=1-2=-1,
故答案为:$\overline{011}$,-1…(4分)
(Ⅱ)当n=3时,所有的3位排列有:
$\overline{000}$,$\overrightarrow{001}$,$\overrightarrow{010}$,$\overrightarrow{100}$,$\overrightarrow{011}$,$\overrightarrow{101}$,$\overrightarrow{110}$,$\overrightarrow{111}$
最佳排列A3为 $\overrightarrow{001}$,$\overrightarrow{010}$,$\overrightarrow{100}$,$\overrightarrow{011}$,$\overrightarrow{101}$,$\overrightarrow{110}$ …(8分)
证明:(Ⅲ)设A5=$\overline{{a}_{1}{a}_{2}{a}_{3}{a}_{4}{a}_{5}}$,则R1(A5)=$\overline{{{a}_{5}a}_{1}{a}_{2}{a}_{3}{a}_{4}}$,
因为 t(A5,R1(A5))=-1,所以|a1-a5|,|a2-a1|,|a3-a2|,|a4-a3|,|a5-a4|之中有2个0,3个1.
按a5→a1→a2→a3→a4→a5的顺序研究数码变化,由上述分析可知有2次数码不发生改变,
有3次数码发生了改变.
但是a5经过奇数次数码改变不能回到自身,所以不存在A5,使得t(A5,R1(A5))=-1,
从而不存在最佳排列A5. …(12分)
点评 本题主要考查排列、组合以及简单计数原理的应用,体现了分类讨论的数学思想,属于难题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
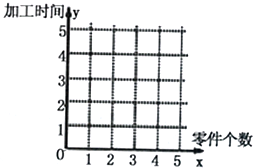 某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如表:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
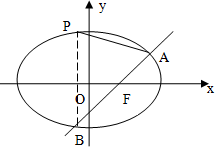 已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b>0)$的离心率为$e=\frac{1}{2}$,直线x+2y-1=0经过椭圆的一个焦点;
已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1,(a>b>0)$的离心率为$e=\frac{1}{2}$,直线x+2y-1=0经过椭圆的一个焦点;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{2}+{y^2}=1$ | B. | (x-1)2+y2=1 | C. | y=x2 | D. | x2-y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
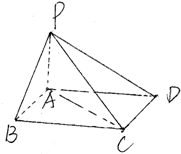 如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD
如图四棱锥P-ABCD中,底面ABCD为平行四边形,∠ABC=60°,PA=AB=1,BC=2,PA⊥底面ABCD查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com