
分析 (Ⅰ)设h(x)=2x2+3x-1=m(x2+ax)+n(x+b),展开后整理,由系数相等把a,b用n表示,然后结合n的范围求得a+2b的取值范围;
(Ⅱ)设h(x)=m(log4(4x+1))+n(x-1),h(x)是偶函数,则h(-x)-h(x)=0,可得m与n的关系,h(x)有最小值则必有n<0,且有-2n=1,求出m和n值,可得解析式
解答 解:(Ⅰ)h(x)=2x2+3x+1=mf(x)+ng(x)=m(x2+ax)+n(x+b)=mx2+(ma+n)x+nb$⇒\left\{{\begin{array}{l}{m=2\;\;}\\{ma+n=3}\\{nb=1\;}\end{array}}\right.⇒2a+\frac{1}{b}=3$,
所以$a+2b=\frac{3}{2}-\frac{1}{2b}+2b$,易知上式递增,
所以$a+2b∈[\frac{3}{2},\;3]$.
(Ⅱ)设h(x)=m(log4(4x+1))+n(x-1),
因为h(x)是偶函数,
所以h(-x)-h(x)=0,
即m(log4(4-x+1))+n(-x-1)-m(log4(4x+1))-n(x-1)=0,
所以(m+2n)x=0,可得:m=-2n.
所以h(x)=-2nlog4(4x+1)+n(x-1)=n(-2nlog4(4x+1)+x-1)=n(log4$\frac{{4}^{x}}{({4}^{x}+1)^{2}}$-1)=n(log4$\frac{1}{{4}^{x}+\frac{1}{{4}^{x}}+2}$-1),
因为$\frac{1}{{4}^{x}+\frac{1}{{4}^{x}}+2}$≤$\frac{1}{4}$,
所以log4$\frac{1}{{4}^{x}+\frac{1}{{4}^{x}}+2}$-1≤-2,
由题意h(x)≥1,
解得n=-$\frac{1}{2}$,从而m=1,
∴h(x)=log4(4x+1)-$\frac{1}{2}$(x-1).
点评 本题考查了函数恒成立问题,考查了数学转化思想方法,训练了利用导数求函数的最值,关键是对题意的理解与合理转化,是压轴题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2、 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
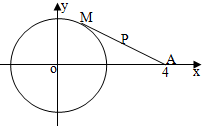 已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,
已知点M是⊙O:x2+y2=4上一动点,A(4,0),点P为线段AM的中点,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com