
已知在四棱锥 中,
中, ,
, ,
, ,
, 分别是
分别是 的中点.
的中点.
(Ⅰ)求证 ;
;
(Ⅱ)求证 ;
;
(Ⅲ)若 ,求二面角
,求二面角 的大小.
的大小.
(1)根据已知条件,要证明 ,则要根据线面你垂直的判定定理来得到,分析
,则要根据线面你垂直的判定定理来得到,分析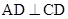 ,所以
,所以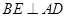 以及
以及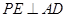 加以证明。
加以证明。
(2) 对于线面平行, 的证明分析到
的证明分析到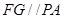 ,是关键一步。
,是关键一步。
(3) 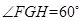 ,所以二面角
,所以二面角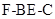 等于
等于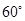
解析试题分析:(Ⅰ) 证明:由已知得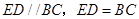 ,
,
故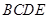 是平行四边形,所以
是平行四边形,所以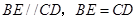 ,---------1分
,---------1分
因为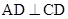 ,所以
,所以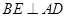 , ---------2分
, ---------2分
由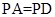 及
及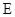 是
是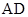 的中点,得
的中点,得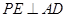 , ---------3分
, ---------3分
又因为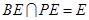 ,所以
,所以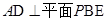 . ---------4分
. ---------4分
(Ⅱ) 证明:连接 交
交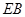 于
于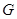 ,再连接
,再连接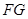 ,
,
由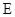 是
是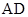 的中点及
的中点及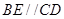 ,知
,知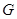 是
是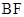 的中点,
的中点,
又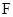 是
是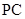 的中点,故
的中点,故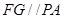 , ---------5分
, ---------5分
又因为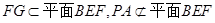 ,
,
所以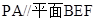 . ---------7分
. ---------7分
(Ⅲ)解:设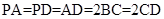
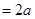 ,
,
则 ,又
,又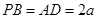 ,
,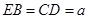 ,
,
故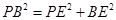 即
即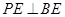 , ---------8分
, ---------8分
又因为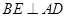 ,
,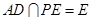 ,
,
所以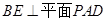 ,得
,得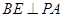 ,故
,故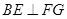 , ---------10分
, ---------10分
取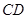 中点
中点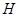 ,连接
,连接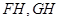 ,可知
,可知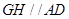 ,因此
,因此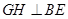 , ---------11分
, ---------11分
综上可知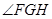 为二面角
为二面角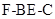 的平面角. ---------12分
的平面角. ---------12分
可知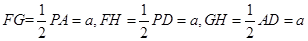 ,
,
故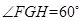 ,所以二面角
,所以二面角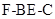 等于
等于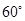 . ---------13分
. ---------13分
考点:线面平行和垂直证明,二面角的平面角
点评:对于空间中的线面的平行和垂直的判定定理以及性质定理要熟练的掌握,是解题的关键,属于中档题。


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
如图梯形ABCD,AD∥BC,∠A=900,过点C作CE∥AB,AD=2BC,AB=BC,,现将梯形沿CE
折成直二面角D-EC-AB.
(1)求直线BD与平面ABCE所成角的正切值;
(2)设线段AB的中点为 ,在直线DE上是否存在一点
,在直线DE上是否存在一点 ,使得
,使得 ∥面BCD?若存在,请指出点
∥面BCD?若存在,请指出点 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图:在多面体EF-ABCD中,四边形ABCD是平行四边形,△EAD为正三角形,且平面EAD 平面ABCD,EF∥AB, AB=2EF=2AD=4,
平面ABCD,EF∥AB, AB=2EF=2AD=4, .
.
(Ⅰ)求证:BF AD;
AD;
(Ⅱ)求直线BD与平面BCF所成角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成30o的二面角 ,如图二,在二面角
,如图二,在二面角 中.
中.
(1) 求D、C之间的距离;
(2) 求CD与面ABC所成的角的大小;
(3) 求证:对于AD上任意点H,CH不与面ABD垂直。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直角梯形ABCD中,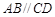 ,
,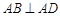 ,且
,且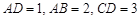 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且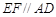 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.
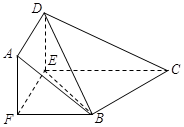
(Ⅰ)求证: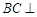 平面BDE;
平面BDE;
(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
如图,四边形 为矩形,
为矩形, 平面
平面 ,
, 为
为 上的点,且
上的点,且 平面
平面 .
.
(1)求证: ;
;
(2)求三棱锥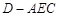 的体积;
的体积;
(3)设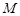 在线段
在线段 上,且满足
上,且满足 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得 平面
平面 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com