
 ��֪��ԲC1��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�����ҽ���ֱ�ΪF��F�䣬˫����C2��$\frac{x^2}{{{a^2}-{b^2}}}-\frac{y^2}{b^2}$=1����ԲC1�ڵ�һ����һ������ΪP���������ĸ����ۣ�
��֪��ԲC1��$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1��{a��b��0}��$�����ҽ���ֱ�ΪF��F�䣬˫����C2��$\frac{x^2}{{{a^2}-{b^2}}}-\frac{y^2}{b^2}$=1����ԲC1�ڵ�һ����һ������ΪP���������ĸ����ۣ�| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
���� �������⣬д��F�䡢F��B1�������꣬ͨ��������Բ��˫���ߵķ��̼���P�ڵ�һ���ޣ��ɵ�P��$\frac{a\sqrt{2��{a}^{2}-{b}^{2}����2{a}^{2}-{b}^{2}��}}{2{a}^{2}-{b}^{2}}$��$\frac{{b}^{2}\sqrt{2{a}^{2}-{b}^{2}}}{2{a}^{2}-{b}^{2}}$������ͨ������$\overrightarrow{PF}•\overrightarrow{P{F^'}}$��
S��PFF�����ɵâ���ȷ���ڵ�a=$\sqrt{2}$bʱ��ͨ������ɵ�cos����PF��F-��PFF�䣩=cos��PF��Fcos��PFF��+sin��PF��Fsin��PFF��=0���ʢ���ȷ���۾ٳ���������a=$\sqrt{2}$bʱ���������ʢ۲���ȷ�� ��ֱ�Ӽ��������C1��C2�������ʼ��ɢ���ȷ��
��� �⣺�������⣬��F�䣨$\sqrt{{a}^{2}-{b}^{2}}$��0����F��-$\sqrt{{a}^{2}-{b}^{2}}$��0����B1��0��b����
������Բ��˫���ߵķ���$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{\frac{{x}^{2}}{{a}^{2}-{b}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$����ȥy����${x}^{2}=\frac{2{a}^{2}��{a}^{2}-{b}^{2}��}{2{a}^{2}-{b}^{2}}$��
�֡ߵ�P�ڵ�һ���ޣ���P��$\frac{a\sqrt{2��{a}^{2}-{b}^{2}����2{a}^{2}-{b}^{2}��}}{2{a}^{2}-{b}^{2}}$��$\frac{{b}^{2}\sqrt{2{a}^{2}-{b}^{2}}}{2{a}^{2}-{b}^{2}}$����
��$\overrightarrow{PF}•\overrightarrow{P{F^'}}$=��-$\sqrt{{a}^{2}-{b}^{2}}$-$\frac{a\sqrt{2��{a}^{2}-{b}^{2}����2{a}^{2}-{b}^{2}��}}{2{a}^{2}-{b}^{2}}$��-$\frac{{b}^{2}\sqrt{2{a}^{2}-{b}^{2}}}{2{a}^{2}-{b}^{2}}$��•��$\sqrt{{a}^{2}-{b}^{2}}$-$\frac{a\sqrt{2��{a}^{2}-{b}^{2}����2{a}^{2}-{b}^{2}��}}{2{a}^{2}-{b}^{2}}$��-$\frac{{b}^{2}\sqrt{2{a}^{2}-{b}^{2}}}{2{a}^{2}-{b}^{2}}$��
=2$\frac{{a}^{2}��{a}^{2}-{b}^{2}��}{2{a}^{2}-{b}^{2}}$-��a2-b2��+$\frac{{b}^{4}}{2{a}^{2}-{b}^{2}}$
=$\frac{{a}^{2}{b}^{2}}{2{a}^{2}-{b}^{2}}$��0��
������PFF������Ϊ$\frac{1}{2}|F��F|y$=$\sqrt{{a}^{2}-{b}^{2}}$��$\frac{{b}^{2}\sqrt{2{a}^{2}-{b}^{2}}}{2{a}^{2}-{b}^{2}}$��b2���ʢ���ȷ��
�ڵ�a=$\sqrt{2}$bʱ����a2=2b2����F�䣨b��0����F��-b��0����$P��\frac{2\sqrt{3}b}{3}��\frac{\sqrt{3}b}{3}��$��
��$\overrightarrow{F��P}$=��$\frac{2\sqrt{3}-3}{3}b$��$\frac{\sqrt{3}b}{3}$����$\overrightarrow{FP}$=��$\frac{2\sqrt{3}+3}{3}b$��$\frac{\sqrt{3}b}{3}$����$\overrightarrow{F��F}$=��-2b��0����
��$|\overrightarrow{F��P}|$=$\frac{\sqrt{6}��\sqrt{3}-1��b}{3}$��$|\overrightarrow{FP}|$=$\frac{\sqrt{6}��\sqrt{3}+1��b}{3}$��$|\overrightarrow{F��F}|$=2b��
��cos��PF��F=$\frac{\overrightarrow{F��F}•\overrightarrow{F��P}}{|\overrightarrow{F��F}||\overrightarrow{F��P}|}$=$\frac{\sqrt{2}-\sqrt{6}}{4}$��cos��PFF��=$\frac{\overrightarrow{FF��}•\overrightarrow{FP}}{|\overrightarrow{FF��}||\overrightarrow{FP}|}$=$\frac{\sqrt{2}+\sqrt{6}}{4}$��
��sin��PF��F=$\frac{\sqrt{2}+\sqrt{6}}{4}$��sin��PFF��=$\frac{\sqrt{6}-\sqrt{2}}{4}$��$\frac{\sqrt{2}-\sqrt{6}}{4}$���ᣩ��
��cos����PF��F-��PFF�䣩=cos��PF��Fcos��PFF��+sin��PF��Fsin��PFF��
=$\frac{\sqrt{2}-\sqrt{6}}{4}$��$\frac{\sqrt{2}+\sqrt{6}}{4}$+$\frac{\sqrt{2}+\sqrt{6}}{4}$��$\frac{\sqrt{6}-\sqrt{2}}{4}$=0��
���PF��F-��PFF��=$\frac{��}{2}$���ʢ���ȷ��
�۵�a=$\sqrt{2}$bʱ���߶�PF���е�ΪM��$\frac{2\sqrt{3}-3}{6}b$��$\frac{\sqrt{3}}{6}b$����
��OM=$\frac{\sqrt{6}��\sqrt{3}-1��b}{6}$��MF=$\frac{\sqrt{6}��\sqrt{3}+1��}{6}b$��OF=2b��
��MF-OF=$\frac{\sqrt{6}��\sqrt{3}+1��}{6}b$-2b��$\frac{\sqrt{6}��\sqrt{3}-1��b}{6}$=OM���ʢ۲���ȷ��
������C1��C2�������ʷֱ�Ϊ��
e1=$\frac{\sqrt{{a}^{2}-{b}^{2}}}{a}$��e2=$\frac{\sqrt{{a}^{2}-{b}^{2}+{b}^{2}}}{\sqrt{{a}^{2}-{b}^{2}}}$=$\frac{a}{\sqrt{{a}^{2}-{b}^{2}}}$���ʢ���ȷ��
��������������٢ڢ���ȷ��
��ѡ��B��
���� ���⿼��Բ���ߵļ����ʣ��������������㣬������������㹫ʽ�����Ǻ�����ǹ�ʽ���е����깫ʽ��Բ��Բ��λ�ù�ϵ������������⡢����������������������������������⣮


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{\sqrt{2}}{2}$] | B�� | ��0��$\frac{\sqrt{6}}{3}$] | C�� | [$\frac{\sqrt{2}}{2}$��$\frac{\sqrt{6}}{3}$] | D�� | [$\frac{\sqrt{6}}{3}$��1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ���ADC�����Բ��BC�ڵ�E��AB=2AC=6��EC=6����AD�ij�Ϊ$\frac{3}{2}$��
��ͼ���ڡ�ABC�У�CD�ǡ�ACB�Ľ�ƽ���ߣ���ADC�����Բ��BC�ڵ�E��AB=2AC=6��EC=6����AD�ij�Ϊ$\frac{3}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ھ���ABCD�У�AB=$\sqrt{2}$��BC=2����EΪBC���е㣬��F�ڱ�CD�ϣ���$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$����$\overrightarrow{AE}$•$\overrightarrow{AF}$��
��ͼ���ھ���ABCD�У�AB=$\sqrt{2}$��BC=2����EΪBC���е㣬��F�ڱ�CD�ϣ���$\overrightarrow{AB}$•$\overrightarrow{AF}$=$\sqrt{2}$����$\overrightarrow{AE}$•$\overrightarrow{AF}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
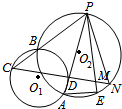 ��ͼ����֪��O1���O2�ཻ��A��B���㣬P�ǡ�O1��һ�㣬PB���ӳ��߽���O2�ڵ�C��PA����O2�ڵ�D��CD���ӳ��߽���O1�ڵ�N��
��ͼ����֪��O1���O2�ཻ��A��B���㣬P�ǡ�O1��һ�㣬PB���ӳ��߽���O2�ڵ�C��PA����O2�ڵ�D��CD���ӳ��߽���O1�ڵ�N���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com