
分析 (1)利用直线和圆的位置关系、抛物线的几何性质,求得圆及抛物线的方程.
(2)利用导数的几何意义求得MA、MB的方程,可得AB的方程,把AB的方程代入圆的方程,利用韦达定理以及两个向量的数量积的运算法则,求得$\overrightarrow{OE}$•$\overrightarrow{OF}$的解析式,可得$\overrightarrow{OE}$•$\overrightarrow{OF}$的范围.
解答 解:(1)∵圆C1:x2+y2=r2(r>0),抛物线C2:x2=2py(p>0)的准线为y=-$\frac{p}{2}$,
点($\sqrt{2}$,-2)是圆C1与抛物线C2准线l的一个交点,
∴-$\frac{p}{2}$=-2,∴p=4,抛物线C2:x2=2py,即x2=8y.
再根据r=$\sqrt{{(\sqrt{2})}^{2}{+(-2)}^{2}}$=$\sqrt{6}$,可得圆C1:x2+y2=6.
(2)若点M是直线l上的动点,设点M(t,-2),A (x1,y1)、B(x2,y2),E(x3,y3)、F(x4,y4),
抛物线C2:x2=8y(p>0),即y=$\frac{{x}^{2}}{8}$,y′=$\frac{x}{4}$,故AM的方程为y-y1=$\frac{{x}_{1}}{4}$(x-x1),
把(t,-2)代入,可得y1=$\frac{t}{4}$x1+2.
同理可得,BM的方程为y2=$\frac{t}{4}$x2+2,∴直线AB的方程为y=$\frac{t}{4}$x+2.
把AB的方程代入圆圆C1:x2+y2=6,可得(1+$\frac{{t}^{2}}{16}$)x2+tx-2=0,
由题意可得△>0,x3+x4=-$\frac{16t}{16{+t}^{2}}$,x3•x4=-$\frac{32}{16{+t}^{2}}$,
∴$\overrightarrow{OE}$•$\overrightarrow{OF}$=x3•x4+y3•y4=(1+$\frac{{t}^{2}}{16}$)x3•x4+$\frac{t}{2}$(x3+x4 )+4
=(1+$\frac{{t}^{2}}{16}$)•(-$\frac{32}{16{+t}^{2}}$)+$\frac{t}{2}$•(-$\frac{16t}{16{+t}^{2}}$ )+4=$\frac{128}{16{+t}^{2}}$-6,
∵0<$\frac{128}{16{+t}^{2}}$≤8,∴$\overrightarrow{OE}$•$\overrightarrow{OF}$的范围为(-6,2].
点评 本题主要考查直线和圆的位置关系、抛物线的几何性质,导数的几何意义,两个向量的数量积的运算,韦达定理,属于中档题.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:选择题
| A. | $y=2\sqrt{2}x+1$ | B. | $y=\sqrt{3}x+1$ | C. | $y=\sqrt{2}x+1$ | D. | $y=2\sqrt{3}x+2$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
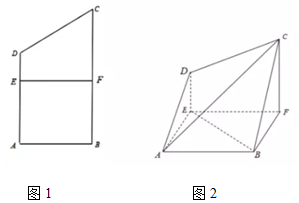 已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.
已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$-1 | B. | $\frac{\sqrt{3}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com