练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知一个60°的二面角的棱上有两点A，B，AC，BD分别是在这个二面角的两个面内垂直于AB的线段，若AB=4，AC=6，BD=8，则CD=（　　）
    A、2
    		41
    B、2
    		3
    C、2
    		17
    D、10
    考点：与二面角有关的立体几何综合题
    专题：综合题,空间位置关系与距离
    分析：由已知可得
    CD
    =
    CA
    +
    AB
    +
    BD
    ，利用数量积的性质即可得出．
    解答： 解：∵CA⊥AB，BD⊥AB，∴
    CA
    •
    AB
    =
    BD
    •
    AB
    =0，
    ∵＜
    AC
    ，
    BD
    ＞    =60°，∴＜
    CA
    ，
    BD
    ＞    =120°．
    ∵
    CD
    =
    CA
    +
    AB
    +
    BD
    ，
    ∴
    CD
    2=
    CA
    2+
    AB
    2+
    BD
    2+2
    CA
    •
    AB
    +2
    CA
    •
    BD
    +2
    AB
    •
    BD

    =62+42+82+0+2×6×8×cos120°+0
    =68．
    ∴|
    CD
    |=2
    		17
    ．
    故选：C．
    点评：熟练掌握向量的运算和数量积运算是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    棱长为4的正方体内切球的表面积为（　　）
    A、4πB、16π
    C、8πD、12π

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若集合M=（y|y=x2-2x+1}，N={x|y=x+
    		2x
    +2}，则M与N的关系是（　　）
    A、M=NB、M≠N
    C、M∈ND、M⊆N

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    若将集合A中的数按从小到大排成数列{an}，则有a1=31+2×0=3，a2=32+2×0=9，a3=32+2×1=11，a4=33+2×0=27，…，依此类推，将数列依次排成如图所示的三角形数阵，则第六行第三个数为（　　）
    A、247B、735
    C、731D、733

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知双曲线
    x2
    64
    -
    y2
    36
    =1上点P到右焦点的距离为14，则其到左焦点距离（　　）
    A、30B、30或2
    C、6或22D、22

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    数列{an}满足a1=
    5
    2
    ，an+1=
    5an-8
    2an-3
    （n∈N*），bn=
    1
    an-2

    （Ⅰ）证明：数列{bn}为等差数列；
    （Ⅱ）已知cn=bn（-
    9
    10
    ）n，求数列{cn}的最大项为第几项；
    （Ⅲ）设Sn为{bn}的前n项和，dn=[
    Sn
    n+4
    ]，其中[x]为不超过x的最大整数，求数列{dn}的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

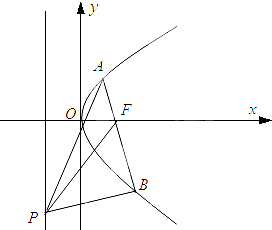    已知抛物线y2=2px（p＞0）上点M（3，m）到焦点F的距离为4．
    （Ⅰ）求抛物线方程；
    （Ⅱ）点P为准线上任意一点，AB为抛物线上过焦点的任意一条弦，设直线PA，PB，PF的斜率为k1，k2，k3，问是否存在实数λ，使得k1+k2=λk3恒成立．若存在，请求出λ的值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆C的焦点坐标分别为（
    		3
    ，0）（-
    		3
    ，0），长轴是短轴的两倍． 
    （1）求椭圆C的方程； 
    （2）在y的正半轴上是否存在一点P（0，p），过定点P作任意一条直线与椭圆C交于两点S，T，使得
    OS
    •
    OT
    为一个定值．若存在，请求出点P的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

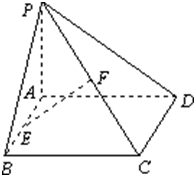    已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、PC的中点，且PA=AD．
    （1）求证：EF∥平面PAD；
    （2）求证：面PEC⊥面PCD．

    查看答案和解析>>

    同步练习册答案