
| A. | 垂心 | B. | 内心 | C. | 外心 | D. | 重心 |
分析 由条件利用平面向量基本定理及其几何意义,求得$\overrightarrow{AI}$=-$\frac{bc}{ab+c}$•($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$),故点I在∠BAC的平分线上;同理可得点I在∠BCA的平分线上;再利用三角形的内心的性质,得出结论.
解答 解:由题意可得$\overrightarrow{IB}$=$\overrightarrow{IA}$+$\overrightarrow{AB}$,$\overrightarrow{IC}$=$\overrightarrow{IA}$+$\overrightarrow{AC}$,
∴a$\overrightarrow{IA}$+b$\overrightarrow{IB}$+c$\overrightarrow{IC}$=a$\overrightarrow{IA}$+b($\overrightarrow{IA}$+$\overrightarrow{AB}$)+c($\overrightarrow{IA}$+$\overrightarrow{AC}$)=(a+b+c)$\overrightarrow{IA}$+b•$\overrightarrow{AB}$+c•$\overrightarrow{AC}$=$\overrightarrow{0}$.
∴(a+b+c)$\overrightarrow{IA}$=-(b•$\overrightarrow{AB}$+c•$\overrightarrow{AC}$ ),
∴$\overrightarrow{IA}$=-($\frac{-(b•\overrightarrow{AB}+c•\overrightarrow{AC})}{a+b+c}$)=-($\frac{b}{a+b+c}$•$\overrightarrow{AB}$+$\frac{c}{a+b+c}$•$\overrightarrow{AC}$ ),
=-$\frac{1}{a+b+c}$(b•$\overrightarrow{AB}$+c•$\overrightarrow{AC}$ )=-$\frac{1}{a+b+c}$(|$\overrightarrow{AC}$|•$\overrightarrow{AB}$+|$\overrightarrow{AB}$|•$\overrightarrow{AC}$ )=-$\frac{bc}{a+b+c}$($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$).
故 $\overrightarrow{IA}$在角A的平分线上,故点I在∠BAC的平分线上.
同理可证,点I在∠BCA的平分线上,故点I为△ABC的内心,
故选:B.
点评 本题主要考查平面向量基本定理及其几何意义,三角形的内心的性质,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
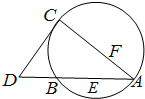 如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a17=0 | B. | a6+a12=0 | C. | S17>0 | D. | a9<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
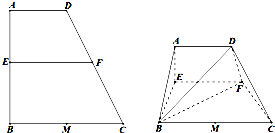 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=90°,AB=BC=2AD=4,M是BC边的中点,E,F分别是AB,CD上的点,且EF∥BC,设AE=x.如图,沿EF将四边形AEFD折起,使平面AEFD⊥平面EBCF.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,2] | B. | (-1,2) | C. | [-1,2] | D. | (-2,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | |a+b|>|a-b| | B. | |a|+|b|>|a-b| | C. | |a-c|≤|a-b|+|b-c| | D. | |a-b|<|a|-|b| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com