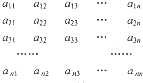Question

17．如图所示，将n²（n≥9）个正数排成n行n列的数阵，其中的每一行都成等差数列，每一列都成等比数列，各等比数列的公比都相同且不为1，若a₁₁=a₂₂=a₃₄=$\frac{1}{2}$，则a₁₁+a₂₂+a₃₃+…+a₉₉=（　　）

• A． $\frac{1031}{512}$
• B． $\frac{1031}{512}$
• C． $\frac{1013}{1024}$
• D． $\frac{1031}{1024}$

Answer 1

分析 根据等比数列、等差数列的定义求得q，进而可知a_nn=$\frac{n}{2}×（\frac{1}{2}）^{n-1}$=$\frac{n}{{2}^{n}}$，进而根据错位相减法求得结论．

解答 解：设公比为q，因为a₁₁=a₂₂=a₃₄=$\frac{1}{2}$，所以a₂₁=$\frac{1}{2}$q，a₃₁=$\frac{1}{2}$q²，a₃₂=$\frac{1}{2}$q．
由a₃₁，a₃₂，a₃₃，a₃₄成等差数列，有a₃₄=a₃₁+3（a₃₂-a₃₁），得q=1（舍）或q=$\frac{1}{2}$．
所以a₁₂=1，a_1n=$\frac{n}{2}$，a_nn=$\frac{n}{2}×（\frac{1}{2}）^{n-1}$=$\frac{n}{{2}^{n}}$，
所以a₁₁+a₂₂+a₃₃+…+a₉₉=$\frac{1}{2}$+$\frac{2}{{2}^{2}}$+…+$\frac{9}{{2}^{9}}$，
由错位相减法可得a₁₁+a₂₂+a₃₃+…+a₉₉=$\frac{1013}{512}$．
故选：B．

点评 本题主要考查等差数列、等比数列的性质，考查错位相减法，考查了学生综合分析问题的能力．