
分析 (1)求出函数的导数,根据f′(1)=0,求出a的值,检验即可;
(2)结合题意得到$a=\frac{{2{e^{x_0}}}}{x_0}$,x0>0.设$g(x)=\frac{{2{e^x}}}{x}$,x>0,根据函数的单调性求出a的范围即可.
解答 解:(1)x>0时,f'(x)=2ex-2x+2a,
依题意有f'(1)=2(e-1+a)=0,得a=1-e,
经验证,0<x<1时,f'(x)=2(ex-x+1-e)<0,
x>1时,f'(x)>0,满足极值要求.
(2)依题意,设存在f(x)=2ex-x2+2ax(x>0)图象上一点(x0,y0),
使得(-x0,-y0)在f(x)=x2+3ax(x<0)的图象上,
则有$\left\{\begin{array}{l}{y_0}=2{e^{x_0}}-x_0^2+2a{x_0},\;\;\\-{y_0}={(-{x_0})^2}+3a(-{x_0}),\;\;\end{array}\right.$
得$2{e^{x_0}}-x_0^2+2a{x_0}=-x_0^2+3a{x_0}$,
化简得:$a=\frac{{2{e^{x_0}}}}{x_0}$,x0>0.
设$g(x)=\frac{{2{e^x}}}{x}$,x>0,则$g'(x)=\frac{{2{e^x}}}{x^2}(x-1)$,
当0<x<1时,g'(x)<0,当x>1时,g'(x)>0,
则g(x)在(0,1)上为减函数,在(1,+∞)上为增函数,
g(x)min=g(1)=2e,
又x→0或x→+∞时,g(x)→+∞,∴g(x)∈[2e,+∞).
所以,a≥2e时,函数y=f(x)的图象上存在两点关于原点对称.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道综合题.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:高中数学 来源: 题型:选择题
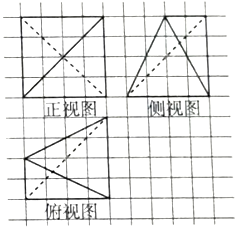
| A. | 8$\sqrt{3}$ | B. | $\frac{80}{3}$ | C. | 16$\sqrt{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0,$\frac{1}{2}$,0,0,$\frac{1}{2}$ | B. | 0.1,0.2,0.3,0.4 | ||
| C. | p,1-p(0≤p≤1) | D. | $\frac{1}{1×2}$,$\frac{1}{2×3}$,…,$\frac{1}{7×8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(?q) | C. | (?p)∧(?q) | D. | (?p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com