
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
科目:高中数学 来源: 题型:解答题
| 月平均气温x(℃) | 17 | 13 | 8 | 2 |
| 月销售量y(件) | 34 | 43 | 50 | 65 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数X | X<150 | 150≤X<350 | 350≤X<450 | X≥450 |
| 暂停工程队数Y | 0 | 2 | 6 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 丁酉年 | B. | 戊未年 | C. | 乙未年 | D. | 丁未年 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4,+∞) | B. | (0,$\frac{5}{2}$] | C. | [$\frac{5}{2}$,4] | D. | [$\frac{5}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
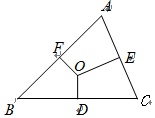 如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,则OD:OE:OF等于( )
如图,在△ABC中,BC=a,AC=b,AB=c.O是△ABC的外心,OD⊥BC于D,OE⊥AC于E,OF⊥AB于F,则OD:OE:OF等于( )| A. | a:b:c | B. | $\frac{1}{a}:\frac{1}{b}:\frac{1}{c}$ | C. | sinA:sinB:sinC | D. | cosA:cosB:cosC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com