
分析 设正方体ABCD-A1B1C1D1的棱长为4,以D为原点,分别以DA、DC、DD1为x、y、z轴建立空间直角坐标系,再设M(x,y,z),利用|MD1|≥2|MP|得出M的轨迹是以B为球心,r=2$\sqrt{3}$的球及其内部,计算对应的体积比,利用几何概率求出概率值.
解答 解:设正方体ABCD-A1B1C1D1的棱长为4,
以D为原点,分别以DA、DC、DD1为x、y、z轴建立空间直角坐标系,
如图所示;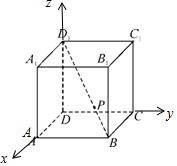
则P(3,3,1),D1(0,0,4),
设M(x,y,z),则|MD1|=$\sqrt{{x}^{2}{+y}^{2}{+(z-4)}^{2}}$,
|MP|=$\sqrt{{(x-3)}^{2}{+(y-3)}^{2}{+(z-1)}^{2}}$,
由|MD1|≥2|MP|,得
$\sqrt{{x}^{2}{+y}^{2}{+(z-4)}^{2}}$≥2$\sqrt{{(x-3)}^{2}{+(y-3)}^{2}{+(z-1)}^{2}}$,
整理得$\sqrt{{(x-4)}^{2}{+(y-4)}^{2}{+(z-0)}^{2}}$≤2$\sqrt{3}$,
即M的轨迹是以B为球心,r=2$\sqrt{3}$的球及其内部,
在正方体中,相当于$\frac{1}{8}$球体,
∴VM=$\frac{1}{8}$×$\frac{4}{3}$π•r3=4$\sqrt{3}π$;
又V正方体=43=64,
∴在正方体内随机取一点M,点M满足MD1≥2ME的概率为
P=$\frac{{V}_{M}}{{V}_{正方体}}$=$\frac{{\sqrt{3}π}}{16}$.
故答案为:$\frac{\sqrt{3}π}{16}$.
点评 本题考查了几何概型的概率计算问题,也考查了对应体积的比值问题,是综合题.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(?q) | C. | (?p)∧(?q) | D. | (?p)∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A∩B | B. | ∁U(A∩B) | C. | A∪(∁UB) | D. | ∁U(A∪B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com