练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．某市有10个施工队，施工期间由于雾霾的影响要对10个工程队采取暂停施工的措施，根据以往经验，空气质量指数X（AQI）与暂停施工队数Y之间有如下关系：
     空气质量指数X X＜150 150≤X＜350 350≤X＜450 X≥450
     暂停工程队数Y 0 2 6 10
    历年气象资料表明，工程施工期间空气质量指数X小于150，350，450的概率分别为0.3，0.7，0.9．
    （1）求暂停工程队数Y的均值和方差；
    （2）在空气质量指数X至少是150的条件下，求暂停工程队数不超过6个的概率．

    分析 （1）根据概率加法公式可得：P（X＜150）=0.3，P（150≤X＜350）=0.7-0.3，P（350≤X＜450）=0.9-0.7．P（450≤X）=1-0.9．即可得出分布列与数学期望．
    （2）P（Y≤6|X≥150）=P（X＜450|X≥150）=$\frac{P（150≤X≤450）}{P（X≥150）}$．

    解答 解：（1）根据概率加法公式可得：P（X＜150）=0.3，P（150≤X＜350）=0.7-0.3=0.4．P（350≤X＜450）=0.9-0.7=0.2．
    P（450≤X）=1-0.9=0.1．

     Y 0 2 6 10
     P 0.3 0.4 0.20.1 
    可得：EY=0+2×0.4+6×0.2+10×0.1=3．
    （2）P（Y≤6|X≥150）=P（X＜450|X≥150）=$\frac{P（150≤X≤450）}{P（X≥150）}$=$\frac{0.6}{0.7}$=$\frac{6}{7}$．

    点评 本题考查了概率加法公式、互斥事件、古典概率计算公式、随机变量的分布列及其数学期望计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    3．设函数f（x）=2x3-3（a+1）x2+6ax+8，其中a∈R．已知f（x）在x=3处的导数为0．
    （1）求f（x）的解析式；       
    （2）求f（x）在点A（1，16）处的切线方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．如图为体积是3的几何体的三视图，则正视图的x值是（　　）
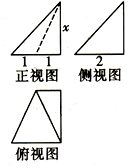
    A．2B．$\frac{9}{2}$C．$\frac{3}{2}$D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知命题p：将函数$f（x）=2sin（{2x+\frac{π}{3}}）$的图象向右平移$\frac{π}{4}$个单位，得到函数g（x）的图象，则函数g（x）在区间$[{-\frac{π}{3}，0}]$上单调递增；命题q：定义在R上的函数y=f（x）满足f（-x）=f（3+x），则函数图象关于直线$x=\frac{3}{2}$对称，则正确的命题是（　　）
    A．p∧qB．p∧（?q）C．（?p）∧（?q）D．（?p）∧q

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数$f（x）=xlnx-x+\frac{1}{2}{x^2}-\frac{1}{3}a{x^3}$，令f（x）的导函数为y=g（x）．
    （I）判定y=g（x）在其定义域内的单调性；
    （II）若曲线y=f（x）上存在两条倾斜角为锐角且互相平行的切线，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．已知P是圆C：x2+y2=4上的动点，P在x轴上的射影为P′，点M满足$\overrightarrow{PM}$=$\overrightarrow{MP′}$，当P在圆C上运动时，点M的轨迹为曲线E．
    （Ⅰ）求曲线E的方程；
    （Ⅱ）经过点A（0，2）的直线l与曲线E相交于点C，D，并且$\overrightarrow{AC}$=$\frac{3}{4}$$\overrightarrow{AD}$，求直线l的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．已知B、C为单位圆上不重合的两定点，A为此单位圆上的动点，若点P满足$\overrightarrow{AP}=\overrightarrow{PB}+\overrightarrow{PC}$，则点P的轨迹为（　　）
    A．椭圆B．双曲线C．抛物线D．圆

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知全集U=R，$A=\left\{{x\left|{-2＜x＜\frac{1}{2}}\right.}\right\}，B=\left\{{x\left|{x≤0}\right.}\right\}，C=\left\{{x\left|{x≥\frac{1}{2}}\right.}\right\}$，则集合C=（　　）
    A．A∩BB．∁U（A∩B）C．A∪（∁UB）D．∁U（A∪B）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知函数f（x）=ex-ax2-2x-1，若曲线y=f（x）在点（1，f（1））处的切线为l，且l在y轴上的截距为-2，则实数a=-1．

    查看答案和解析>>

    同步练习册答案