练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．已知函数f（x）=ex-ax2-2x-1，若曲线y=f（x）在点（1，f（1））处的切线为l，且l在y轴上的截距为-2，则实数a=-1．

    分析 求出导数，求得切线的斜率和切点，再由两点的斜率公式，解方程可得a的值．

    解答 解：函数f（x）=ex-ax2-2x-1的导数为f′（x）=ex-2ax-2，
    在点（1，f（1））处的切线斜率为e-2a-2，
    切点为（1，e-a-3），又切线过（0，-2），
    则e-2a-2=$\frac{e-a-3+2}{1-0}$，解得a=-1；
    故答案为：-1．

    点评 本题考查了切线方程问题，考查导数的应用，是一道基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    13．某市有10个施工队，施工期间由于雾霾的影响要对10个工程队采取暂停施工的措施，根据以往经验，空气质量指数X（AQI）与暂停施工队数Y之间有如下关系：
     空气质量指数X X＜150 150≤X＜350 350≤X＜450 X≥450
     暂停工程队数Y 0 2 6 10
    历年气象资料表明，工程施工期间空气质量指数X小于150，350，450的概率分别为0.3，0.7，0.9．
    （1）求暂停工程队数Y的均值和方差；
    （2）在空气质量指数X至少是150的条件下，求暂停工程队数不超过6个的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

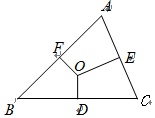    14．如图，在△ABC中，BC=a，AC=b，AB=c．O是△ABC的外心，OD⊥BC于D，OE⊥AC于E，OF⊥AB于F，则OD：OE：OF等于（　　）
    A．a：b：cB．$\frac{1}{a}：\frac{1}{b}：\frac{1}{c}$C．sinA：sinB：sinCD．cosA：cosB：cosC

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知不等式|x-2|＜|x|的解集为（$\frac{m}{2}$，+∞）
    （1）求实数m的值
    （2）若不等式a-5＜|x+1|-|x-m|＜a+2对x∈（0，+∞）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．曲线y=eaxcosx在x=0处的切线与直线x+2y=0垂直，则a=（　　）
    A．-2B．-1C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．设F1、F2分别是双曲线${x^2}-\frac{y^2}{4}=1$的左、右焦点，点P在双曲线上，且|PF1|=5，则|PF2|=（　　）
    A．1B．3C．3或7D．1或9

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．复数$z={（{\frac{1-i}{1+i}}）^4}+2i$的共轭复数$\overline z$=-1-2i．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

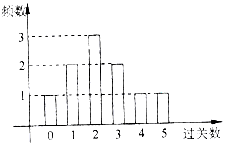    12．某学校在一次第二课堂活动中，特意设置了过关智力游戏，游戏共五关．规定第一关没过者没奖励，过n（n∈N*）关者奖励2n-1件小奖品（奖品都一样）．如图是小明在10次过关游戏中过关数的条形图，以此频率估计概率．
    （Ⅰ）估计小明在1次游戏中所得奖品数的期望值；
    （II）估计小明在3次游戏中至少过两关的平均次数；
    （Ⅲ）估计小明在3次游戏中所得奖品超过30件的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右焦点分别为F1、F2，过F2的直线与椭圆交于A、B两点，若△F1AB是等边三角形，则离心率为（　　）
    A．$\frac{\sqrt{2}}{2}$B．$\frac{1}{3}$C．$\frac{\sqrt{3}}{3}$D．$\frac{3}{4}$

    查看答案和解析>>

    同步练习册答案