
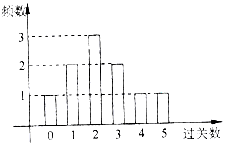
 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.分析 (Ⅰ)设小明在1次游戏中所得奖品数为ξ,根据题意写出ξ 的分布列,
计算期望值;
(Ⅱ)设小明在3次游戏中至少过两关的次数为X,则X~B(3,0.7),
计算E(X)即可;
(Ⅲ)计算小明在3次游戏中所得奖品超过30件的概率值即可.
解答 解:(Ⅰ)设小明在1次游戏中所得奖品数为ξ,则ξ 的分布列为
| ξ | 0 | 1 | 2 | 4 | 8 | 16 |
| P | 0.1 | 0.2 | 0.3 | 0.2 | 0.1 | 0.1 |
点评 本题考查了离散型随机变量的分布列与数学期望的计算问题,是综合题.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:高中数学 来源: 题型:选择题
| A. | A∩B | B. | ∁U(A∩B) | C. | A∪(∁UB) | D. | ∁U(A∪B) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 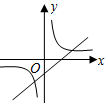 | B. | 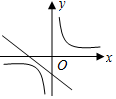 | C. | 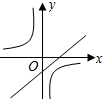 | D. | 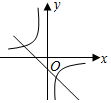 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com