
| A. | 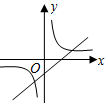 | B. | 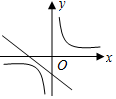 | C. | 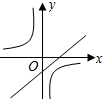 | D. | 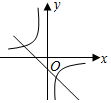 |
分析 根据两函数图象所过的象限进行逐一分析,再进行选择即可.
解答 解:A、由函数y=ax+b过一、三、四象限可知,a>0,b<0;由函数y=$\frac{a+b}{x}$图象可知,a+b>0,与已知a>b,且a≠0,b≠0,a+b≠0,相吻合,故可能成立;
B、由直线的图象知a<0,b<0,故a+b<0,所以y=$\frac{a+b}{x}$的图象在二四象限,
C、由函数y=ax+b过一、三、四象限可知,a>0,b<0;由函数y=$\frac{a+b}{x}$的图象可知,a+b<0,与已知a>b,且a≠0,b≠0,a+b≠0,相吻合,故可能成立;
D、由函数y=ax+b过一、三、四象限可知,a<0,b<0;由函数y=$\frac{a+b}{x}$的图象可知,a+b<0,与已知a>b,且a≠0,b≠0,a+b≠0,相吻合,故可能成立;
故选:B.
点评 本题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
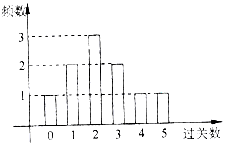 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,5] | B. | [1,5] | C. | (0,5) | D. | [1,25] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com