
分析 根据题意得出a>0,对应二次函数图象的对称轴为x=-$\frac{1}{a}$=c,且△=4-4ab=0,化$\frac{{a}^{2}{+b}^{2}+1}{a+c}$=(a-b)+$\frac{3}{a-b}$,利用基本不等式求出最值,即可求出结果.
解答 解:根据关于x的一元二次不等式ax2+2x+b>0的解集为{x|x≠c},
可得a>0,对应的二次函数的图象的对称轴为x=-$\frac{1}{a}$=c,且△=4-4ab=0,
∴ac=-1,ab=1,
∴c=-$\frac{1}{a}$,b=$\frac{1}{a}$,
∴c=-b;
∴$\frac{{a}^{2}{+b}^{2}+1}{a+c}$=$\frac{{(a-b)}^{2}+3}{a-b}$=(a-b)+$\frac{3}{a-b}$;
当a-b>0时,由基本不等式求得(a-b)+$\frac{3}{a-b}$≥2$\sqrt{3}$,
当a-b<0时,由基本不等式求得-(a-b)-$\frac{3}{a-b}$≥2$\sqrt{3}$,
即(a-b)+$\frac{3}{a-b}$≤-2$\sqrt{3}$
故$\frac{{a}^{2}{+b}^{2}+1}{a+c}$(其中a+c≠0)的取值范围为:(-∞,-2$\sqrt{3}$]∪[2$\sqrt{3}$,+∞),
故答案为:(-∞,-2$\sqrt{3}$]∪[2$\sqrt{3}$,+∞).
点评 本题主要考查了二次函数的性质与基本不等式的应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 3 | C. | 3或7 | D. | 1或9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 4 | C. | 6 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
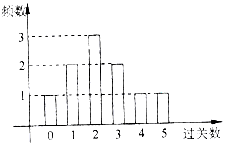 某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.
某学校在一次第二课堂活动中,特意设置了过关智力游戏,游戏共五关.规定第一关没过者没奖励,过n(n∈N*)关者奖励2n-1件小奖品(奖品都一样).如图是小明在10次过关游戏中过关数的条形图,以此频率估计概率.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com