
| 月平均气温x(℃) | 17 | 13 | 8 | 2 |
| 月销售量y(件) | 34 | 43 | 50 | 65 |
分析 (1)分别求出样本的中心点,求出方程的系数$\widehat{b}$,$\widehat{a}$的值,求出回归方程即可;(2)将x=3代入方程求出函数的预报值即可.
解答 解:(1)$\overline{x}=(17+13+8+2)÷4=10$,$\overline{y}=(34+43+50+65)÷4=48$,
$\sum_{i=1}^4{{x_i}{y_i}}=17×34+13×43+8×50+2×65=1667$,$\sum_{i=1}^4{x_i^2}=526$,
$\widehat{b}$=$\frac{1667-4×10×48}{{526-4×{{10}^2}}}=-2.01≈-2.0$,$a=\bar y-b\overline{x}=48-(-2.01)×10≈68.1$,
∴线性回归方程为$\widehat{y}$=-2.0x+68,1;
(2)气象部门预测下个月的平均气温约为3℃,
据此估计,该商场下个月毛衣的销售量为:
$\widehat{y}$=-2.0x+68.1=-2.0×3+68.1≈62(件)
点评 本题考查了求回归方程问题,考查函数求值问题,是一道基础题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$<a<1 | B. | a>1或a$<-\frac{1}{3}$ | C. | -1$<a<\frac{1}{3}$ | D. | a$>\frac{1}{3}$或a<-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
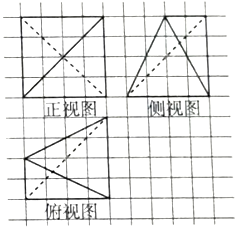
| A. | 8$\sqrt{3}$ | B. | $\frac{80}{3}$ | C. | 16$\sqrt{3}$ | D. | 32 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0,$\frac{1}{2}$,0,0,$\frac{1}{2}$ | B. | 0.1,0.2,0.3,0.4 | ||
| C. | p,1-p(0≤p≤1) | D. | $\frac{1}{1×2}$,$\frac{1}{2×3}$,…,$\frac{1}{7×8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆 | B. | 双曲线 | C. | 抛物线 | D. | 圆 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com