
【题目】如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 为梯形,
为梯形,![]() ,
,![]() ,且
,且![]() .
.

(Ⅰ)若点![]() 为
为![]() 上一点且
上一点且![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,说明理由.
的长;若不存在,说明理由.
【答案】(Ⅰ)见解析;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
试题分析:(Ⅰ)要证线面平行,就要证线线平行,由线面平行的性质定理知平行线是过![]() 的平面
的平面![]() 与平面
与平面![]() 的交线,由已知过点
的交线,由已知过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,![]() 就是要找的平行线;(Ⅱ)求二面角,由于图中已知
就是要找的平行线;(Ⅱ)求二面角,由于图中已知![]() 两两垂直,因此以它们为坐标轴建立空间直角坐标系,可用向量法求得二面角,只要求得两个面的法向量,由法向量的夹角与二面角相等或互补可得(需确定二面角是锐二面角还是钝二面角);(3)有了第(2)小题的空间直角坐标系,因此解决此题时,假设存在点
两两垂直,因此以它们为坐标轴建立空间直角坐标系,可用向量法求得二面角,只要求得两个面的法向量,由法向量的夹角与二面角相等或互补可得(需确定二面角是锐二面角还是钝二面角);(3)有了第(2)小题的空间直角坐标系,因此解决此题时,假设存在点![]() ,设
,设![]() ,由
,由![]() 求得
求得![]() 即可.
即可.
试题解析:(Ⅰ)过点![]() 作
作![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,
,
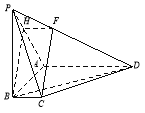
因为![]() ,所以
,所以![]() .
.
又![]() ,
,![]() ,所以
,所以![]() .
.
所以![]() 为平行四边形, 所以
为平行四边形, 所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,(一个都没写的,则这1分不给)
,(一个都没写的,则这1分不给)
所以![]() 平面
平面![]() .
.
(Ⅱ)因为梯形![]() 中,
中,![]() ,
,![]() ,所以
,所以![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
如图,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
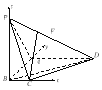
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,
,
因为![]()
所以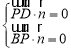 ,即
,即![]() ,
,
取![]() 得到
得到![]() ,
,
同理可得![]() ,
,
所以![]() ,
,
因为二面角![]() 为锐角,
为锐角,
所以二面角![]() 为
为![]() .
.
(Ⅲ)假设存在点![]() ,设
,设![]() ,
,
所以![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以存在点![]() ,且
,且![]() .
.


科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示,甲的成绩中有一个数的个位数字模糊,在茎叶图中用![]() 表示.(把频率当作概率).
表示.(把频率当作概率).
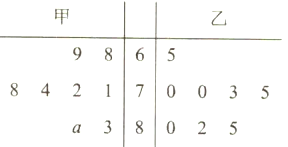
(1)假设![]() ,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
,现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
(2)假设数字![]() 的取值是随机的,求乙的平均分高于甲的平均分的概率.
的取值是随机的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+log2x+b在区间( ![]() ,4)上有零点,则实数b的取值范围是( )
,4)上有零点,则实数b的取值范围是( )
A.(﹣10,0)
B.(﹣8,1)
C.(0,10)
D.(1,12)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比小于1的等比数列{an}的前n项和为Sn , a1= ![]() 且13a2=3S3(n∈N*).
且13a2=3S3(n∈N*).
(1)求数列{an}的通项公式;
(2)设bn=nan , 求数列{bn}的前项n和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 对一切实数
对一切实数![]() 都有
都有![]()
![]() 成立,且
成立,且![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)已知![]() ,设
,设![]() :当
:当![]() 时,不等式
时,不等式![]() 恒成立;Q:当
恒成立;Q:当![]() 时,
时,![]() 是单调函数。如果满足
是单调函数。如果满足![]() 成立的
成立的![]() 的集合记为
的集合记为![]() ,满足Q成立的
,满足Q成立的![]() 的集合记为
的集合记为![]() ,求A∩(CRB)(
,求A∩(CRB)(![]() 为全集).
为全集).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个班级共有105名学生,某次数学考试按照“大于等于85分为优秀,85分以下为非优秀”的原则统计成绩后,得到如下![]() 列联表。
列联表。
优秀 | 非优秀 | 总计 | |
甲班 | 10 | ||
乙班 | 30 | ||
总计 | 105 |
已知从甲、乙两个班级中随机抽取1名学生,其成绩为优秀的概率为![]() .
.
(1)请完成上面的![]() 列联表;
列联表;
(2)能否有把握认为成绩与班级有关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com