Question

16．如图，已知点C是圆心为O半径为1的半圆弧上从点A数起的第一个三等分点AB是圆O的直径，CD=1，且CD⊥平面ABC，E是AD的中点
（1）求证：AC⊥BD；
（2）求点C到平面ABD的距离．
（3）求二面角O-EC-B的余弦值．

Answer 1

分析 （1）证明AC⊥平面BCD，即可证明AC⊥BD；
（2）建立空间坐标系，方法一：利用向量法即可求点C到平面ABD的距离．
方法二：根据点到平面的定义求出点到平面的垂线段，即可．
（3）求出平面的法向量，利用向量法即可求二面角O-EC-B的余弦值．

解答 证明：（1）∵CD⊥平面ABC，AC?平面ABC，
∴CD⊥AC．
∵点C在圆O上，AB是直径，
∴AC⊥BC．
又∵CD∩BC=C，
∴AC⊥平面BCD．
又∵BD?平面BCD，
∴AC⊥BD．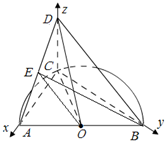
解：∵C是圆心为O半径为1的半圆弧上
从点A数起的第一个三等分点，
∴∠AOC=60°，
∴△OAC是等边三角形，
∴CA=CD=1．
∵C是圆周上的点，AB是直径，
∴AC⊥AB，
∴CB=$\sqrt{A{B}^{2}-A{C}^{2}}$=$\sqrt{3}$，
又CD⊥平面ABC，
∴AC，BC，CD两两垂直．以点C为坐标原点，CA，CB，CD分别为x、y、z轴的正向，建立空间直角坐标系，
则A（1，0，0），B（0，$\sqrt{3}$，0），C（0，0，0），D（0，0，1），E（$\frac{1}{2}$，0，$\frac{1}{2}$），O（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，0），
（2）方法一：$\overrightarrow{AB}$=（-1，$\sqrt{3}$，0），$\overrightarrow{AD}$=（-1，0，1），$\overrightarrow{CD}$=（0，0，1），
设$\overrightarrow{h}$=（x₁，y₁，z₁）为平面ABD的法向量，
则$\left\{\begin{array}{l}\overrightarrow{h}•\overrightarrow{AB}=0\\ \overrightarrow{h}•\overrightarrow{AD}=0\end{array}\right.$，即$\left\{\begin{array}{l}{-x}_{1}+\sqrt{3}{y}_{1}=0\\{-x}_{1}+{z}_{1}=0\end{array}\right.$，
取y₁=$\sqrt{3}$，得$\overrightarrow{h}$=（3，$\sqrt{3}$，3）．
设向量$\overrightarrow{h}$和$\overrightarrow{CD}$ 所成的角为?，
则cos?=$\frac{|\overrightarrow{h}•\overrightarrow{CD}|}{\left|\overrightarrow{h}\right|•\left|\overrightarrow{CD}\right|}$=$\frac{\sqrt{21}}{7}$，
设点C到平面ABD的距离为d，则d=|$\overrightarrow{CD}$|cos?=$\frac{\sqrt{21}}{7}$．
方法二：由（1）知AC=1，BC=$\sqrt{3}$，
因为直线CD⊥平面ABC，所以，CD⊥AC，CD⊥BC，
于是，AD=$\sqrt{{AC}^{2}+{CD}^{2}}$=$\sqrt{2}$，BD=$\sqrt{{BC}^{2}+{CD}^{2}}$=2．
因为AB=2=BD，点E是AD的中点，所以BE⊥AD．
因此，BE=$\sqrt{{AB}^{2}-{AE}^{2}}$=$\frac{\sqrt{14}}{2}$，
从而，S_△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$，
S_△ABD=$\frac{1}{2}$AD•BE=$\frac{1}{2}$×$\sqrt{2}$×$\frac{\sqrt{14}}{2}$=$\frac{\sqrt{7}}{2}$．
因为，V_C-ABD=V_D-ABC，
设点C到平面ABD的距离为h，
则有$\frac{1}{3}$S_△ABD•h=$\frac{1}{3}$S_△ABC•CD，
即$\frac{\sqrt{7}}{2}$•h=$\frac{\sqrt{3}}{2}$×1，
于是，h=$\frac{\sqrt{21}}{7}$．
（3）$\overrightarrow{CB}$=（0，$\sqrt{3}$，0），$\overrightarrow{CE}$=（$\frac{1}{2}$，0，$\frac{1}{2}$），$\overrightarrow{CO}$=（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$，0）．
设$\overrightarrow{n}$=（x，y，z）为平面BCE的法向量，$\overrightarrow{m}$=（p，q，r）为平面OCE的法向量，
由$\overrightarrow{n}$•$\overrightarrow{CB}$=0⇒y=0，$\overrightarrow{n}$•$\overrightarrow{CE}$=0⇒$\frac{1}{2}$x+$\frac{1}{2}$z=0，
取x=1得$\overrightarrow{n}$=（1，0，-1）．
由$\overrightarrow{m}$•$\overrightarrow{CE}$=0⇒$\frac{1}{2}$p+$\frac{1}{2}$r=0，$\overrightarrow{m}$•$\overrightarrow{CO}$=0⇒$\frac{1}{2}$p+$\frac{\sqrt{3}}{2}$q=0，
取p=1得$\overrightarrow{m}$=（1，-$\frac{\sqrt{3}}{3}$，-1）
cosθ=$\frac{|\overrightarrow{m}•\overrightarrow{n}|}{\left|\overrightarrow{m}\right|•\left|\overrightarrow{n}\right|}$=$\frac{\sqrt{42}}{7}$，
因此，二面角O-EC-B的余弦值是$\frac{\sqrt{42}}{7}$．

点评 本题主要考查二面角的求解以及点到平面的距离的计算，建立坐标系，利用向量法是解决空间二面角和点到平面距离的常用方法．