
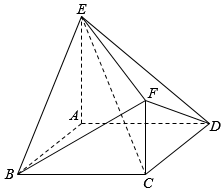
 如图,已知多面体ABCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.
如图,已知多面体ABCDEF中,ABCD为菱形,∠ABC=60°,AE⊥平面ABCD,AE∥CF,AB=AE=1,AF⊥BE.分析 (I)由AE∥CF,可得四点ACFE共面.如图所示,连接AC,BD,相交于点O,利用菱形对角线的性质及其线面垂直的判定及其性质可得:AE⊥平面ABCD,可得BD⊥平面ACFE,BD⊥AF,可得AF⊥平面BDE,即可证明.
(II)取BC的中点M,由∠ABC=60°,AB=BC,可得△ABC是等边三角形,AM⊥BC,AM⊥AD,建立空间直角坐标系,利用AF⊥BE,可得F坐标.设平面ABF的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{AF}=0}\end{array}\right.$,可得取$\overrightarrow{m}$.同理可得:平面AFD的法向量$\overrightarrow{n}$,利用向量夹角公式即可得出.
解答  (I)证明:∵AE∥CF,∴四点ACFE共面.
(I)证明:∵AE∥CF,∴四点ACFE共面.
如图所示,连接AC,BD,相交于点O,
∵四边形ABCD是菱形,∴对角线BD⊥AC,
∵AE⊥平面ABCD,
∴AE⊥BD,又AE∩AC=A,
∴BD⊥平面ACFE,
∴BD⊥AF,
又AF⊥BE,BE∩BD=B,
∴AF⊥平面BDE,
AF?平面BAF,
∴平面BAF⊥平面BDE.
(II)解:取BC的中点M,∵∠ABC=60°,AB=BC,
∴△ABC是等边三角形,∴AM⊥BC,又BC∥AD,
∴AM⊥AD,建立空间直角坐标系,
A(0,0,0),B$(\frac{\sqrt{3}}{2},-\frac{1}{2},0)$,F$(\frac{\sqrt{3}}{2},\frac{1}{2},z)$,D(0,1,0),E(0,0,1).
$\overrightarrow{AB}$=$(\frac{\sqrt{3}}{2},-\frac{1}{2},0)$,$\overrightarrow{AF}$=$(\frac{\sqrt{3}}{2},\frac{1}{2},z)$,$\overrightarrow{AD}$=(0,1,0),$\overrightarrow{BE}$=$(-\frac{\sqrt{3}}{2},\frac{1}{2},1)$.
∵AF⊥BE.
∴$\overrightarrow{AF}•\overrightarrow{BE}$=$-\frac{3}{4}$+$\frac{1}{4}$+z=0,解得z=$\frac{1}{2}$.
设平面ABF的法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=0}\\{\overrightarrow{m}•\overrightarrow{AF}=0}\end{array}\right.$,∴$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}x-\frac{1}{2}y=0}\\{\frac{\sqrt{3}}{2}x+\frac{1}{2}y+\frac{1}{2}z=0}\end{array}\right.$,取$\overrightarrow{m}$=$(1,\sqrt{3},-2\sqrt{3})$.
同理可得:平面AFD的法向量$\overrightarrow{n}$=$(1,0,-\sqrt{3})$.
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{7}{2×4}$=$\frac{7}{8}$.
由图可知:二面角B-AF-D的平面角为钝角,
∴二面角B-AF-D的余弦值为-$\frac{7}{8}$.
点评 本题考查了空间位置关系、空间角、向量垂直与数量积的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 圆的面积与半径具有相关性 | B. | 纯净度与净化次数不具有相关性 | ||
| C. | 作物的产量与人的耕耘是负相关 | D. | 学习成绩与学习效率是正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
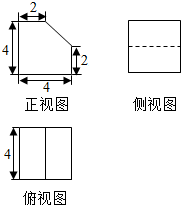
| A. | 84 | B. | $76+8\sqrt{2}$ | C. | $78+8\sqrt{2}$ | D. | $80+8\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
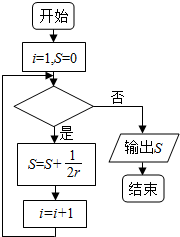
| A. | i≤1006 | B. | i≤1007 | C. | i>1007 | D. | i>1006 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com