
【题目】已知函数![]() ,其中
,其中![]() ;
;
(l)判断函数![]() 是否存在极值,若存在,请判断是极大值还是极小值;若不存在,说明理由;
是否存在极值,若存在,请判断是极大值还是极小值;若不存在,说明理由;
(2)讨论在![]() 上函数
上函数![]() 的零点个数.
的零点个数.
【答案】(1)见解析;(2)见解析
【解析】
(1) ![]() ,设
,设![]() ,
,![]() ,因此
,因此![]() 单调递减,
单调递减,![]() ,讨论
,讨论![]() 正负即可判断出极值情况;
正负即可判断出极值情况;
(2)由(1)可知若![]() 时,
时,![]() 恒为增函数,计算可知
恒为增函数,计算可知![]() ,此时无零点, 若
,此时无零点, 若![]() 时,
时, ![]() ,可求得
,可求得![]() ,讨论
,讨论![]() 与
与![]() 的关系,及若
的关系,及若![]() ,
,![]() ,函数在区间
,函数在区间![]() 的单调性及函数值在区间端点的符号,即可得出结论.
的单调性及函数值在区间端点的符号,即可得出结论.
(1)![]() ,设
,设![]() ,
,
![]() ,因此
,因此![]() 单调递减,
单调递减,
![]() ,
,
又![]() 时,
时,![]() ,
,
若![]() ,即
,即![]() 时,
时,
![]() ,使
,使![]() ;
;
当![]() 时,
时,![]() ,
,![]() 单调递增,
单调递增,
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
![]() 在
在![]() 处取极大值,不存在极小值.
处取极大值,不存在极小值.
若![]() ,即
,即![]() ,
,![]() ,
,
![]() 在
在![]() 单调递增,此时
单调递增,此时![]() 无极值.
无极值.
(2)由第一问结论可知:
(i)若![]() 时,由上问可知:
时,由上问可知:
![]() ,
,
即![]() 时函数没有零点.
时函数没有零点.
(ii)若![]() 时,
时,![]() 时
时![]() 单调递增;
单调递增;
![]() 时,
时,![]() 单调递减.
单调递减.
由![]() ,得
,得![]() ,
,
从而![]() ,再设
,再设![]() ,
,
则![]() ,从而a关于
,从而a关于![]() 单调递增.
单调递增.
①若![]() ,此时
,此时![]() ,
,
若![]() 得
得![]() 或
或![]() ,
,
所以![]() 时无零点;
时无零点;
若![]() 得
得![]() ,
,
所以![]() 时有一个零点;
时有一个零点;
当![]() ,
,![]() ,有一个零点.
,有一个零点.
因此![]() 时无零点;
时无零点;
![]() 时有一个零点;
时有一个零点;
②![]() 此时
此时![]() ,
,
![]() ,
,![]() ,
,
![]()
![]() ,
,
设![]() ,
,
则![]() ,
,
所以![]() ,
,
若![]() 即
即![]() ,即
,即![]() 时无零点;
时无零点;
若![]() 即
即![]() ,即
,即![]() 时有一个零点.
时有一个零点.
综上所述:![]() 时无零点;
时无零点;
![]() 时有一个零点.
时有一个零点.


科目:高中数学 来源: 题型:
【题目】我们正处于一个大数据飞速发展的时代,对于大数据人才的需求也越来越大,其岗位大致可分为四类:数据开发、数据分析、数据挖掘、数据产品.某市2019年这几类工作岗位的薪资(单位:万元/月)情况如下表所示:
薪资
岗位 |
|
|
|
|
数据开发 |
|
|
|
|
数据分析 |
|
|
|
|
数据挖掘 |
|
|
|
|
数据产品 |
|
|
|
|
由表中数据可得该市各类岗位的薪资水平高低情况为( )
A.数据挖掘>数据开发>数据产品>数据分析
B.数据挖掘>数据产品>数据开发>数据分析
C.数据挖掘>数据开发>数据分析>数据产品
D.数据挖掘>数据产品>数据分析>数据开发
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,AB是圆O:x2+y2=1的直径,且点A在第一象限;圆O1:(x﹣a)2+y2=r2(a>0)与圆O外离,线段AO1与圆O1交于点M,线段BM与圆O交于点N,且![]() ,则a的取值范围为_______.
,则a的取值范围为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率,数学发展史上出现过许多很有创意的求法,如著名的浦丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计π的值:先请120名同学每人随机写下一个都小于1的正实数对(x,y)且x+y>1;再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m,最后再根据统计数m估计π的值,假如统计结果是m=72,那么可以估计π的值约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,且a3+a4+a5=28,a4+2是a3,a5的等差中项.数列{bn}满足b1=1,数列{(bn+1﹣bn)an}的前n项和为2n2+n.
(1)求数列{an}的通项公式;
(2)求数列{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学与文学之间存在着奇妙的联系,诗中有回文诗,如“山东落花生花落东山,西湖回游鱼游回湖西”,倒过来读,仍然是原句!数学上也有这样一类数,如66,202,3773,34543,无论从左往右读,还是从右往左读,都是同一个数,我们称这样的数为“回文数”,现用数字1,2,3,4组数(可重复用),则组成的五位“回文数”的个数为( )
A.24B.28C.48D.64
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桥牌是一种高雅、文明、竞技性很强的智力性游戏.近年来,在中国桥牌协会“桥牌进校园”活动的号召下,全国各地中小学纷纷积极加入到青少年桥牌推广的大营中.为了了解学生对桥牌这项运动的兴趣,某校从高一学生中随机抽取了200名学生进行调查,经统计男生与女生的人数之比为2:3,男生中有50人对桥牌有兴趣,女生中有20人对桥牌不感兴趣.
(1)完成2×2列联表,并回答能否有![]() 的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
的把握认为“该校高一学生对桥牌是否感兴趣与性别有关”?
感兴趣 | 不感兴趣 | 合计 | |
男 | 50 | —— | —— |
女 | —— | 20 | —— |
合计 | —— | —— | 200 |
(2)从被调查的对桥牌有兴趣的学生中利用分层抽样抽取6名学生,再从6名学生中抽取2名学生作为桥牌搭档参加双人赛.求抽到一名男生与一名女生的概率.
附:参考公式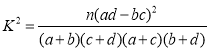 ,其中
,其中![]() .
.
临界值表:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为支援武汉的防疫,某医院职工踊跃报名,其中报名的医生18人,护士12人,医技6人,根据需要,从中抽取一个容量为n的样本参加救援队,若采用系统抽样和分层抽样,均不用剔除人员.当抽取n+1人时,若采用系统抽样,则需剔除1个报名人员,则抽取的救援人员为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com