
已知函数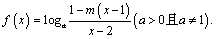
(1) 若 时,判断
时,判断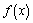 在
在 上的单调性,并说明理由;
上的单调性,并说明理由;
(2) 若对于定义域内一切 ,
,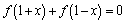 恒成立,求实数
恒成立,求实数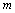 的值;
的值;
(3) 在(2)的条件下,当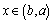 时,
时,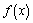 的值域恰为
的值域恰为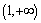 ,求实数
,求实数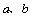 的值.
的值.
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:
如图是2013年某大学自主招生面试环节中,七位评委为某考生打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数和众数依次为( )
A.85,84 B.84,85
C.86,84 D.84,86
查看答案和解析>>
科目:高中数学 来源: 题型:
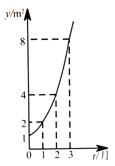
右图所示是某池塘中的浮萍蔓延的面积 与时间
与时间 (月)的关系:
(月)的关系: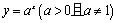 ,有以下叙述:
,有以下叙述:
① 这个指数函数的底数是2;
② 第5个月时,浮萍的面积就会超过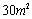 ;
;
③ 浮萍从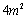 蔓延到
蔓延到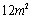 需要经过
需要经过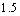 个月;
个月;
④ 浮萍每个月增加 的面积都相等.
其中正确的说法是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
某单位建造一间地面面积为12m2的背面靠墙的矩形小房,由于地理位置的限制,房子侧面的长度x不得超过a米,房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2,屋顶和地面的造价费用合计为5800元,如果墙高为3m, 且不计房屋背面的费用.
且不计房屋背面的费用.
(1)把房屋总造价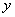 表示成
表示成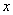 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.
(2)当侧面的长度为多少时,总造价最底?最低总造价是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com