
分析 (1)根据向量的坐标运算和向量的平行即可得到关于k的方程,解得即可
(2)利用向量的线性运算法则及向量相等即可得出.
解答 解:(1)$\overrightarrow{a}$+k$\overrightarrow{c}$=(3,2)+k(4,1)=(3+4k,2+k),
2$\overrightarrow{b}$+$\overrightarrow{c}$=2(-1,2)+(4,1)=(2,5),
∵$(\overrightarrow a+k\overrightarrow c)∥(2\overrightarrow b+n\overrightarrow c)$,
∴5(3+4k)=2(2+k),
解得k=-$\frac{11}{18}$,
(2)$\overrightarrow a=m\overrightarrow b-n\overrightarrow c$,
∴(3,2)=m(-1,2)-n(4,1)=(-m-4n,2m-n),
∴$\left\{\begin{array}{l}{3=-m-4n}\\{2=2m-n}\end{array}\right.$,
解得m=$\frac{5}{9}$,n=-$\frac{8}{9}$
点评 本题考查了向量坐标形式的加减法和数乘法则的综合运算,向量共线的坐标条件,直接代入公式求解.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{39}}}{3}$ | B. | $\frac{26}{3}\sqrt{3}$ | C. | $\frac{8}{3}\sqrt{3}$ | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f′(x)>0,g′(x)<0 | B. | f′(x)>0,g′(x)>0 | C. | f′(x)<0,g′(x)<0 | D. | f′(x)<0,g′(x)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
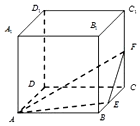 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CC1的中点,P是侧面BCC1B1内一点,若A1P∥平面AEF,则线段AP长度的取值范围是[$\frac{3\sqrt{2}}{4}$,$\frac{\sqrt{5}}{2}$].查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com