
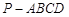 中,底面
中,底面 是平行四边形,
是平行四边形,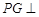 平面
平面 ,垂足为
,垂足为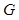 ,
,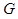 在
在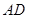 上且
上且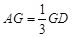 ,
,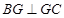 ,
,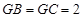 ,
,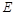 是
是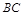 的中点,四面体
的中点,四面体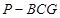 的体积为
的体积为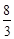 .
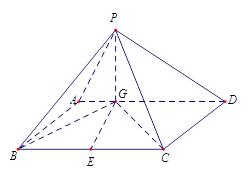
.
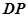 到平面
到平面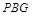 所成角的正弦值;
所成角的正弦值;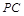 上是否存在一点
上是否存在一点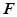 ,使
,使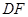
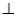
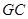 ,若存在,确定点
,若存在,确定点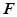 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.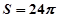 ;(2)
;(2)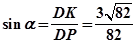 ;(3)存在,
;(3)存在,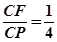 .
.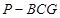 的体积可以求出高
的体积可以求出高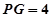 .
.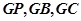 两两垂直,所以以
两两垂直,所以以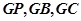 为同一顶点的三条棱构造长方体,长方体的外接球即为过点P,C,B,G四点的球,其直径就是长方体的体对角线.
为同一顶点的三条棱构造长方体,长方体的外接球即为过点P,C,B,G四点的球,其直径就是长方体的体对角线.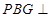 面
面 ,所以只需在面ABCD内过点D作交线BG的垂线,即可得PD在面PBG内的射影,从而得PD与面PBG所成的角. (3)首先假设
,所以只需在面ABCD内过点D作交线BG的垂线,即可得PD在面PBG内的射影,从而得PD与面PBG所成的角. (3)首先假设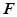 存在,然后确定
存在,然后确定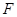 的位置,若能在
的位置,若能在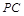 上找到点
上找到点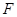 使
使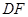
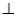
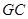 则说明这样的点F存在.
则说明这样的点F存在.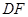 与
与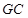 是异面的两条直线,我们通过转化,转化这相交的两条直线的垂直问题.那么如何转化?过
是异面的两条直线,我们通过转化,转化这相交的两条直线的垂直问题.那么如何转化?过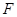 作
作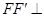
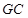 交GC于
交GC于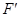 ,则只要
,则只要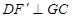 即可.这样确定
即可.这样确定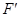 的位置容易得多了.
的位置容易得多了.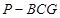 的体积为
的体积为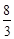 .∴
.∴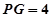 .
.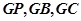 构造长方体,外接球的直径为长方体的体对角线。
构造长方体,外接球的直径为长方体的体对角线。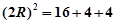 ∴
∴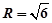
 3分
3分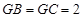
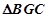 为等腰三角形,GE为
为等腰三角形,GE为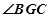 的角平分线,作
的角平分线,作 交BG的延长线于K,
交BG的延长线于K,
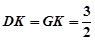 ,
,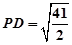 .设直线
.设直线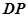 与平面
与平面 所成角为
所成角为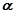
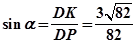 8分
8分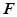 存在,过
存在,过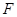 作
作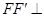
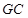 交GC于
交GC于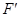 ,则必有
,则必有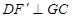 .因为
.因为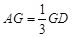 ,且
,且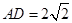 ,所以
,所以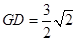 ,又
,又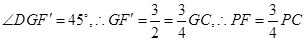 .
.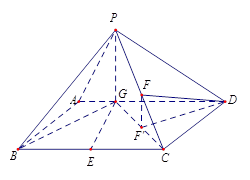
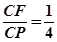 时满足条件 12分
时满足条件 12分

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源:不详 题型:解答题
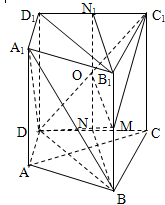
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
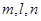 和平面
和平面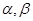 的四个命题:
的四个命题: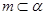 ,
,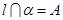 ,点
,点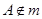 ,则
,则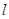 与
与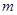 不共面;
不共面;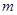 、
、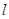 是异面直线,
是异面直线,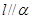 ,
,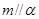 ,且
,且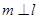 ,
,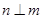 ,则
,则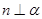 ;
;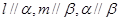 ,则
,则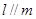 ;
;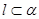 ,
,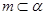 ,
,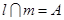 ,
,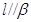 ,
,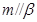 ,则
,则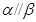 .
.| A.① | B.② | C.④ | D.③ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.若任意四点不共面,则其中任意三点必不共线 |
B.若直线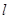 上有一点在平面 上有一点在平面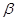 外,则 外,则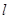 在平面 在平面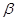 外 外 |
| C.若一个平面内的任一条直线都平行于另一个平面,则这两个平面平行 |
D.若直线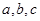 中, 中,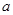 与 与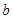 共面且 共面且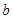 与 与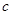 共面,则 共面,则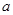 与 与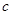 共面 共面 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.底面是正方形,有两个侧面是矩形 |
| B.每个侧面都是全等矩形的四棱柱 |
| C.底面是菱形,且有一个顶点处的三条棱两两垂直 |
| D.底面是正方形,有两个相邻侧面垂直于底面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com