练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．某疾病研究所想知道吸烟与患肺病是否有关，于是随机抽取11000名成年人调查是否抽烟及是否患有肺病得到2×2列联表，经计算得K2=5.231，已知在假设吸烟与患肺病无关的前提条件下，P（K2≥3.841）=0.05，P（K2≥6.635）=0.01，则该研究所可以（　　）
    A．有95%以上的把握认为“吸烟与患肺病有关”
    B．有95%以上的把握认为“吸烟与患肺病无关”
    C．有99%以上的把握认为“吸烟与患肺病有关”
    D．有99%以上的把握认为“吸烟与患肺病无关”

    分析 根据条件中所给的计算出的观测值，把观测值同临界值进行比较，看出有1-0.05=95%的把握认为“吸烟与患肺病有关”，得到结论．

    解答 解：∵计算得K2=5.231，
    经查对临界值表知P（K2≥3.841）≈0.05，
    ∴有1-0.05=95%的把握认为“吸烟与患肺病有关”，
    故选：A．

    点评 本题考查独立性检验，是一个基础题，解决本题的关键是正确理解研究患肺病是否与吸烟有关时，计算出观测值得到概率的意义．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．阅读如图所示的程序框图，运行相应的程序，输出的S=（　　）
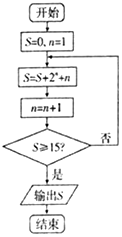
    A．40B．21C．20D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知平面向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（2x+3，-x）（x∈R）．
    （1）若$\overrightarrow{a}$∥$\overrightarrow{b}$，求|$\overrightarrow{a}-\overrightarrow{b}$|
    （2）若$\overrightarrow{a}$与$\overrightarrow{b}$夹角为锐角，求x的取值范围．
    （3）若|$\overrightarrow a}$|=2，求与${\overrightarrow a}$垂直的单位向量$\overrightarrow c$的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．把-1485°化成2kπ+α（0＜α＜2π，k∈Z）的形式是-10π+$\frac{7π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数f（x）=x2+（a+8）x+a2+a-12（a＜0），且f（a2-4）=f（2a-8），则$\frac{f（n）-4a}{n+1}（n∈{N^+}）$的最小值为（　　）
    A．$\frac{37}{4}$B．$\frac{35}{8}$C．$\frac{28}{3}$D．$\frac{27}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若点P（x，y）在线段AB上运动，且A（4，0），B（0，2），设T=log2x+log2y，则（　　）
    A．T有最大值2B．T有最小值1
    C．T有最大值1D．T没有最大值和最小值

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．△ABC的内角A，B，C的对边分别为a，b，c，若其外接圆半径$R=\frac{5}{6}$，$cosB=\frac{3}{5}$，$cosA=\frac{12}{13}$，则c=$\frac{21}{13}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．若椭圆E1：$\frac{x^2}{a_1^2}+\frac{y^2}{b_1^2}=1$与椭圆E2：$\frac{x^2}{a_2^2}+\frac{y^2}{b_2^2}=1$满足$\frac{a_1}{a_2}=\frac{b_1}{b_2}=m（{m＞0}）$，则称这两个椭圆相似，m叫相似比．若椭圆M1与椭圆${M_2}：{x^2}+2{y^2}=1$相似且过$（{1，\frac{{\sqrt{2}}}{2}}）$点．
    （I）求椭圆M1的标准方程；
    （II）过点P（-2，0）作斜率不为零的直线l与椭圆M1交于不同两点A、B，F为椭圆M1的右焦点，直线AF、BF分别交椭圆M1于点G、H，设$\overrightarrow{AF}={λ_1}\overrightarrow{FG}$，$\overrightarrow{BF}={λ_2}\overrightarrow{FH}（{{λ_1}、{λ_2}∈R}）$，求λ1+λ2的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．设函数f（x）是定义在R上的以5为周期的奇函数，若$f（2）＞1，f（3）=\frac{{{a^2}+a+3}}{a-3}$，则a的取值范围是（-∞，-2）∪（0，3）．

    查看答案和解析>>

    同步练习册答案