
【题目】如图,在正方体ABCD﹣A1B1C1D1中,E为DD1的中点.求证: 
(1)BD1∥平面EAC;
(2)平面EAC⊥平面AB1C.
【答案】
(1)证明:连接BD,交AC于O.连接EO,BD1.
因为E为DD1的中点,所以BD1∥OE.)
又OE平面EAC,BD1平面EAC,
所以BD1∥平面EAC
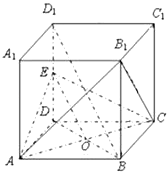
(2)证明:∵BB1⊥AC,BD⊥AC.BB1∩BD=B,BB1、BD在面BB1D1D 内
∴AC⊥平面BB1D1D
又BD1平面BB1D1D∴BD1⊥AC.
同理BD1⊥AB1,∴BD1⊥平面AB1C.
由(1)得BD1∥OE,∴EO⊥平面AB1C.
又EO平面EAC,∴平面EAC⊥平面AB1C
【解析】(1)连接BD,交AC于O.连接EO,BD1 . 根据中位线可知BD1∥OE,又OE平面EAC,BD1平面EAC,根据线面平行的判定定理可知BD1∥平面EAC;(2)根据BB1⊥AC,BD⊥AC,BB1∩BD=B,满足线面垂直的判定定理,则AC⊥平面BB1D1D,又BD1平面BB1D1D则BD1⊥AC,同理BD1⊥AB1 , 从而BD1⊥平面AB1C.根据(1)可得BD1∥OE,从而EO⊥平面AB1C,又EO平面EAC,根据面面垂直的判定定理可知平面EAC⊥平面AB1C.
【考点精析】掌握直线与平面平行的判定和平面与平面垂直的性质是解答本题的根本,需要知道平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直.


科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小张的投篮命中率与打篮球时间之间的关系,下表记录了小张某月1号到5号每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的关系:
之间的关系:
时间 | 1 | 2 | 3 | 4 | 5 |
命中率 | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
(1)求小张这![]() 天的平均投篮命中率;
天的平均投篮命中率;
(2)利用所给数据求小张每天打篮球时间![]() (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率![]() 之间的线性回归方程
之间的线性回归方程![]() ;(参考公式:
;(参考公式:![]() )
)
(3)用线性回归分析的方法,预测小李该月![]() 号打
号打![]() 小时篮球的投篮命中率.
小时篮球的投篮命中率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点C在以AB为直径的圆O上,PA垂直于圆O所在的平面,G为△AOC的重心. 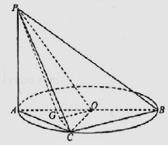
(1)求证:平面OPG⊥平面PAC;
(2)若PA=AB=2AC=2,求二面角A﹣OP﹣G的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线
,左右焦点分别为F1 , F2 , 以椭圆短轴为直径的圆与直线 ![]() 相切.
相切.
(Ⅰ)求椭圆E的方程;
(Ⅱ)过点F1、斜率为k1的直线l1与椭圆E交于A,B两点,过点F2、斜率为k2的直线l2与椭圆E交于C,D两点,且直线l1 , l2相交于点P,若直线OA,OB,OC,OD的斜率kOA , kOB , kOC , kOD满足kOA+kOB=kOC+kOD , 求证:动点P在定椭圆上,并求出此椭圆方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点A(1,﹣1),B(3,0),C(2,1),P为平面ABC上的一点, ![]() =λ
=λ ![]() +μ
+μ ![]() ,且
,且 ![]()
![]() =0,
=0, ![]()
![]() =3.
=3.
(1)求 ![]()
![]() ;
;
(2)求λ+μ 的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】先阅读下列题目的证法,再解决后面的问题.
已知a1,a2∈R,且a1+a2=1,求证:a+a≥![]() .
.
证明:构造函数f(x)=(x-a1)2+(x-a2)2,则f(x)=2x2-2(a1+a2)x+a+a=2x2-2x+a+a.
因为对一切x∈R,恒有f(x)≥0,
所以Δ=4-8(a+a)≤0,从而得a+a≥![]() .
.
(1)若a1,a2,…,an∈R,a1+a2+…+an=1,请由上述结论写出关于a1,a2,…,an的推广式;
(2)参考上述证法,请对你推广的结论加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为调查来自南方和北方的同龄大学生的身高差异,从2016级的年龄在18~19岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下(单位:cm):
南方:158,170,166,169,180,175,171,176,162,163.
北方:183,173,169,163,179,171,157,175,184,166.

(1)根据抽测结果,画出茎叶图,对来自南方和北方的大学生的身高作比较,写出统计结论.
(2)设抽测的10名南方大学生的平均身高为x cm,将10名南方大学生的身高依次输入如图所示的程序框图进行运算,问输出的s大小为多少?并说明s的统计学意义.
(3)为进一步调查身高与生活习惯的关系,现从来自南方的这10名大学生中随机抽取2名身高不低于170 cm的学生,求身高为176 cm的学生被抽中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】冶炼某种金属可以用旧设备和改造后的新设备,为了检验用这两种设备生产的产品中所含杂质的关系,调查结果如下表所示:
分类 | 杂质高 | 杂质低 |
旧设备 | 37 | 121 |
新设备 | 22 | 202 |
根据以上数据,则( )
A. 含杂质的高低与设备改造有关
B. 含杂质的高低与设备改造无关
C. 设备是否改造决定含杂质的高低
D. 以上答案都不对
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com