练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．已知f（x）=$\frac{{2}^{x}}{2（ln2-1）x}$，则f′（1）=1．

    分析 先求导，再代值计算即可．

    解答 解：f′（x）=$\frac{{x•2}^{x}ln2-{2}^{x}}{2（ln2-1）{x}^{2}}$，
    ∴f′（1）=$\frac{2ln2-2}{2（ln2-1）}$=1，
    故答案为：1

    点评 本题考查了导数的运算法则，考查计算能力．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    5．命题p：若1＜y＜x，0＜a＜1，则 ${a^{\frac{1}{x}}}＜{a^{\frac{1}{y}}}$，命题q：若1＜y＜x，a＜0，则xa＜ya．在命题①p且q②p或q③非p④非q中，真命题是（　　）
    A．①③B．①④C．②③D．②④

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．执行如图所示程序框图，若输出的S=-46，则①处填入的条件可以是（　　）
    A．k＜4？B．k＜5？C．k＞4？D．k＞5？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．用数字1，2，3，4，5可以组成没有重复数字，并且比20000大的五位偶数共有36个．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知数列{an}中，a1=1，an+1=$\frac{2（n+1）{a}_{n}}{n}$+n+1．
    （I）求证：数列{$\frac{{a}_{n}}{n}$+1}是等比教列．
    （II）求数列{an}的前n项和为Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

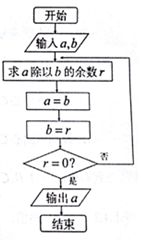    20．我国古代名著《九章算术》用“更相减损术”求两个正整数的最大公约数是一个伟大创举．这个伟大创举与我国古老的算法-“辗转相除法”实质一样．如图的程序框图即源于“辗转相除法”，当输入a=3051，b=1008时，输出的a=（　　）
    A．6B．9C．12D．18

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．为研究男女同学空间想象能力的差异，孙老师从高一年级随机选取了20名男生、20名女生，进行空间图形识别测试，得到成绩茎叶图如下，假定成绩大于等于80分的同学为“空间想象能力突出”，低于80分的同学为“空间想象能力正常”．
    （1）完成下面2×2列联表，并判断是否有90%的把握认为“空间想象能力突出”与性别有关；
    空间想象能力突出空间想象能力正常合计
    男生
    女生
    合计
    （2）从“空间想象能力突出”的同学中随机选取男生2名、女生2名，记其中成绩超过90分的人数为ξ，求随机变量ξ的分布列和数学期望．
    下面公式及临界值表仅供参考：${X^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
    P（X2≥k）0.1000.0500.010
    k2.7063.8416.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

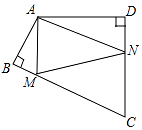    4．如图，四边形ABCD中，∠BAD=120°，∠B=∠D=90°，在BC、CD上分别找一点M、N，使△AMN周长最小时，则∠AMN+∠ANM的度数为（　　）
    A．140°B．130°C．120°D．110°

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

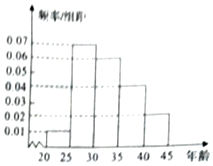    15．某地为增强居民的传统文化意识，活跃节日氛围，在元宵节举办了猜灯谜比赛，现从参加比赛的选手中随机抽取200名后按年龄分组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45），得到的频率分布直方图如图所示．
    （1）若从第3，4，5组中用分层抽样的方法抽取12名选手参加传统知识问答比赛，则应从第3，4，5组各抽取多少名选手？
    （2）在（1）的条件下，该地决定在第4，5组的选手中随机抽取2名选手介绍比赛感想，求第5组至少有一名选手被抽中的概率．

    查看答案和解析>>

    同步练习册答案