
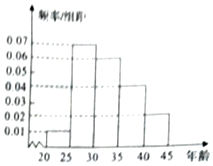
 某地为增强居民的传统文化意识,活跃节日氛围,在元宵节举办了猜灯谜比赛,现从参加比赛的选手中随机抽取200名后按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
某地为增强居民的传统文化意识,活跃节日氛围,在元宵节举办了猜灯谜比赛,现从参加比赛的选手中随机抽取200名后按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.分析 (1)先分别求出这3组的人数,再利用分层抽样的方法即可得出答案;
(2)利用古典概型的概率计算公式、互斥事件及相互独立事件的概率计算公式即可得出.
解答 解:(1)第3组的人数为0.3×200=60,第4组的人数为0.2×200=40,第5组的人数为0.1×200=20,则第3,4,5组共有120名志愿者,所以利用分层抽样的方法在120名志愿者中抽取12名志愿者,每组抽取的人数分别为第3组$\frac{60}{120}×12=6$;第4组$\frac{40}{120}×12=4$;第5组$\frac{20}{120}×12=2$,所以应从第3,4,5组中分别抽取6人,4人,2人.
(2)记第4组的4名志愿者为a,b,c,d,第5组的2名志愿者为A,B,则从6名志愿者中抽取2名志愿者有ab,ac,ad,aA,aB,bc,bd,bA,bB,cd,cA,cB,dA,dB,AB,共15种,其中第5组的2名志愿者A,B中至少有一名志愿者被抽中的有aA,aB,bA,bB,cA,cB,dA,dB,AB,共9种,所以第5组至少有一名志愿者被抽中的概率为$\frac{9}{15}=\frac{3}{5}$.
点评 熟练掌握频率分布直方图、分层抽样的定义、古典概型的概率计算公式、互斥事件及相互独立事件的概率计算公式是解题的关键.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
| x(万元) | 1 | 2 | 3 | 4 | 5 |
| y(万元) | 24 | 30 | 38 | 42 | 51 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a,b∈R,则a-b>0⇒a>b,推出:若a,b∈C,则a-b>0⇒a>b | |
| B. | 若a,b∈R,则a2+b2=0⇒a=b=0,推出:若a,b∈C,则a2+b2=0⇒a=b=0 | |
| C. | 若a,b∈R,则a-b=0⇒a=b,推出:若a,b∈C,则a-b=0⇒a=b | |
| D. | 若x∈R,则|x|<1⇒-1<x<1,推出:若x∈C,则|x|<1⇒-1<x<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
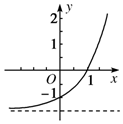 已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,
已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com