
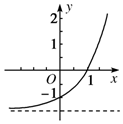
 已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,
已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,分析 (1)由图象得,点(1,0),(0,-1)在函数f(x)的图象上,代值计算即可,
(2)分别画出y=2x-2,y=log2x的图象,由图象可得函数的零点.
解答 解:(1)由图象得,点(1,0),(0,-1)在函数f(x)的图象上,
所以$\left\{\begin{array}{l}{a+b=0}\\{1+b=-1}\end{array}\right.$,
解得$\left\{\begin{array}{l}a=2\\ b=-2\end{array}$
∴f(x)=2x-2.
(2)g(x)=f(x)-logax=2x-2-log2x,其定义域为(0,+∞)
令g(x)=2x-2-log2x=0,
则2x-2=log2x,
分别画出y=2x-2,y=log2x的图象,如图所示,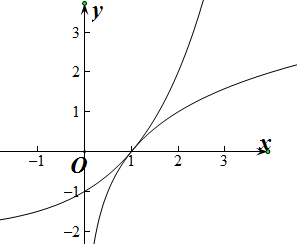
由图象可得,y=2x-2,y=log2x的图象只有一个交点,即x=1,
故存在函数的零点,且零点为1
点评 本题考查了函数的零点存在定理和指数函数和对数函数的定义,属于中档题.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:选择题
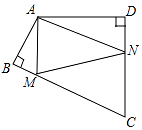 如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )
如图,四边形ABCD中,∠BAD=120°,∠B=∠D=90°,在BC、CD上分别找一点M、N,使△AMN周长最小时,则∠AMN+∠ANM的度数为( )| A. | 140° | B. | 130° | C. | 120° | D. | 110° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
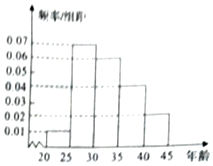 某地为增强居民的传统文化意识,活跃节日氛围,在元宵节举办了猜灯谜比赛,现从参加比赛的选手中随机抽取200名后按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.
某地为增强居民的传统文化意识,活跃节日氛围,在元宵节举办了猜灯谜比赛,现从参加比赛的选手中随机抽取200名后按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45),得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{51}{8}]$ | B. | (-∞,3] | C. | $[\frac{51}{8},+∞)$ | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(1)>ef(0),f(2016)>e2016f(0) | B. | f(1)<ef(0),f(2016)>e2016f(0) | ||
| C. | f(1)>ef(0),f(2016)<e2016f(0) | D. | f(1)<ef(0),f(2016)>e2016f(0) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},\frac{3}{4})$ | B. | $[-\frac{1}{2},\frac{3}{4}]$ | C. | $(-∞,\frac{1}{2}]∪(\frac{3}{4},+∞)$ | D. | $[-\frac{1}{2},\frac{3}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com