
���� ��1��������F1����ԲE�Ķ���������˵����������ε��������㣬��$Q��{\sqrt{3}��\frac{1}{2}}��$����ԲE�ϣ��г����������a��b�ɵ���Բ���̣�
��2����ֱ��l1�ķ���y=tx������$\left\{\begin{array}{l}y=tx\\ \frac{x^2}{4}+\frac{y^2}{1}=1\end{array}\right.$�����$|{GH}|=\sqrt{1+{t^2}}•\frac{4}{{\sqrt{4{t^2}+1}}}$��${d_{{A_1}-{l_1}}}=|{\frac{2t}{{\sqrt{{t^2}+1}}}}|=\frac{2t}{{\sqrt{{t^2}+1}}}$��${d_{{B_1}-{l_1}}}=\frac{1}{{\sqrt{{t^2}+1}}}$���Ƴ��ı���A1GB1H�������������ֵ��Ȼ�����ֱ�߷��̣�
��3����ֱ��l2�ķ���y=k��x+c������Բb2x2+a2y2-a2b2=0��M��x1��y1����N��x2��y2��������Τ�ﶨ�������
����$\overrightarrow{PM}=��\overrightarrow{M{F_1}}$��$\overrightarrow{PN}=��\overrightarrow{N{F_1}}$������+�̼��ɣ�
��� ����С������13�֣�
�⣺��1����F1����ԲE�Ķ���������˵����������ε��������㣬��$Q��{\sqrt{3}��\frac{1}{2}}��$����ԲE�ϣ�
$\left\{\begin{array}{l}c=\sqrt{3}b\\ \frac{3}{a^2}+\frac{1}{{4{b^2}}}=1\\{a^2}-{b^2}={c^2}\end{array}\right.$��3�֣�
��$\left\{\begin{array}{l}{a^2}=4\\{b^2}=1\end{array}\right.$��������Բ����$\frac{x^2}{4}+\frac{y^2}{1}=1$ ��2�֣�
��2����ֱ��l1�ķ���y=tx
����$\left\{\begin{array}{l}y=tx\\ \frac{x^2}{4}+\frac{y^2}{1}=1\end{array}\right.$�����Լ���$|{GH}|=\sqrt{1+{t^2}}•\frac{4}{{\sqrt{4{t^2}+1}}}$��1�֣�
${d_{{A_1}-{l_1}}}=|{\frac{2t}{{\sqrt{{t^2}+1}}}}|=\frac{2t}{{\sqrt{{t^2}+1}}}$��${d_{{B_1}-{l_1}}}=\frac{1}{{\sqrt{{t^2}+1}}}$��1�֣�
${S_{��{A_1}G{B_1}H}}=\frac{1}{2}��{\frac{2t+1}{{\sqrt{{t^2}+1}}}}��•\frac{{4\sqrt{{t^2}+1}}}{{\sqrt{4{t^2}+1}}}$��
��${S_{��{A_1}G{B_1}H}}=\frac{{2��{2t+1}��}}{{\sqrt{4{t^2}+1}}}$��2�֣�
${S^2}_{��{A_1}G{B_1}H}=4��{1+\frac{4}{{4t+\frac{1}{t}}}}����4��{1+\frac{4}{{2\sqrt{4t+\frac{1}{t}}}}}��$��
��$t=\frac{1}{2}��{��{{S_{��{A_1}G{B_1}H}}}��_{max}}=2\sqrt{2}$��
����ֱ��l1�ķ�����$y=\frac{1}{2}x$��2�֣�
��3����ֱ��l2�ķ���y=k��x+c������Բb2x2+a2y2-a2b2=0��M��x1��y1����N��x2��y2����
��b2+a2k2��x2+2a2k2cx+a2k2c2-a2b2=0��
${x_1}+{x_2}=-\frac{{2{a^2}{k^2}c}}{{{a^2}{k^2}+{b^2}}}��{x_1}{x_2}=\frac{{{a^2}{k^2}{c^2}-{a^2}{b^2}}}{{{a^2}{k^2}+{b^2}}}$��2�֣�
ֱ��l2��ֱ��x=-p��p��0���ڵ�P����������$\overrightarrow{PM}=��\overrightarrow{M{F_1}}$��$\overrightarrow{PN}=��\overrightarrow{N{F_1}}$��
�õ���x1+p��yp��=�ˣ�-c-x1��0-y1������x1+p��yp��=�ˣ�-c-x2��0-y2����
��$��=-\frac{{{x_1}+p}}{{{x_1}+c}}$��$��=-\frac{{{x_2}+p}}{{{x_2}+c}}$ ��2�֣�
$��+��=-��{\frac{{{x_1}+p}}{{{x_1}+c}}+\frac{{{x_2}+p}}{{{x_2}+c}}}��=-\frac{{��{{x_1}+p}����{{x_2}+c}��+��{{x_2}+p}����{{x_1}+c}��}}{{��{{x_1}+c}����{{x_2}+c}��}}$
=$-\frac{{2{x_1}{x_2}+��{p+c}����{{x_1}+{x_2}}��+2pc}}{{{x_1}{x_2}+c��{{x_1}+{x_2}}��+{c^2}}}$
=-$\frac{\frac{2{a}^{2}{k}^{2}{c}^{2}-2{a}^{2}{b}^{2}}{{a}^{2}{k}^{2}+{b}^{2}}-��p+c��\frac{2{a}^{2}{k}^{2}c}{{a}^{2}{k}^{2}+{b}^{2}}+2pc}{\frac{{a}^{2}{k}^{2}{c}^{2}-{a}^{2}{b}^{2}}{{a}^{2}{k}^{2}+{b}^{2}}-\frac{2{a}^{2}{k}^{2}c}{{a}^{2}{k}^{2}+{b}^{2}}+{c}^{2}}$
=-$\frac{2pc{b}^{2}-2{a}^{2}{b}^{2}}{-{b}^{4}}$
=$\frac{2pc-2{a}^{2}}{{b}^{2}}$
=$\frac{{2��{p\sqrt{{a^2}-{b^2}}-{a^2}}��}}{b^2}$��3�֣�
��+�̵�ֵΪ��$\frac{{2��{p\sqrt{{a^2}-{b^2}}-{a^2}}��}}{b^2}$���ۣ�1�֣�
���� ���⿼����Բ���̵���ֱ������Բ��λ�ù�ϵ��Ӧ�ã�����ת��˼���Լ�����������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
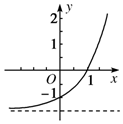 ��֪����f��x��=ax+b��a��0����a��1������f��x����ͼ����ͼ��ʾ��
��֪����f��x��=ax+b��a��0����a��1������f��x����ͼ����ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| x ��g�� | 5 | 10 | 15 | 20 | 25 | 30 |
| y ��cm�� | 7.25 | 8.12 | 8.95 | 9.90 | 10.9 | 11.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
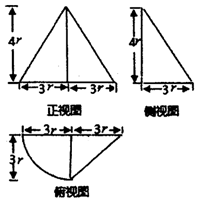 ��֪һ�����ε�����ͼ��ͼ��ʾ�����ü���������Ϊ24��+48����ü�����ı����Ϊ��������
��֪һ�����ε�����ͼ��ͼ��ʾ�����ü���������Ϊ24��+48����ü�����ı����Ϊ��������| A�� | 24��+48 | B�� | $24��+90+6\sqrt{41}$ | C�� | 48��+48 | D�� | $24��+66+6\sqrt{41}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -1 | C�� | -3 | D�� | 3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3��223 | B�� | 3��224 | C�� | 223 | D�� | 224 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 132 | B�� | 66 | C�� | -132 | D�� | -66 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com