
分析 (1)求出f(x)的导数,由题意可得f′($\frac{1}{2}$)=0,解得a的值,可得f(x)和导数f′(x),由导数大于0,可得增区间;导数小于0,可得减区间;进而得到f(x)的极小值;
(2)运用基本不等式求出f(x)在[0,2]的值域,求出g(x)的导数,由题意可得极值点在(1,2)内,求出g(x)在[1,2]的最小值,比较g(1)和g(2)的值,可得g(x)的最大值,由题意可得f(x),g(x)的值域无交集,即可得到k的取值范围.
解答 解:(1)函数f(x)=$\frac{x-a}{{x}^{2}+1}$的导数为f′(x)=$\frac{-{x}^{2}+2ax+1}{(1+{x}^{2})^{2}}$,
由f(x)的一个极值点为$\frac{1}{2}$,可得f′($\frac{1}{2}$)=0,
即为a+1-$\frac{1}{4}$=0,解得a=-$\frac{3}{4}$,
则f(x)=$\frac{x+\frac{3}{4}}{1+{x}^{2}}$,f′(x)=$\frac{-{x}^{2}-\frac{3}{2}x+1}{(1+{x}^{2})^{2}}$=-$\frac{1}{2}$•$\frac{(2x-1)(x+2)}{(1+{x}^{2})^{2}}$,
由f′(x)>0,解得-2<x<$\frac{1}{2}$;由f′(x)<0,解得x<-2或x>$\frac{1}{2}$.
可得f(x)的增区间为(-2,$\frac{1}{2}$),减区间为(-∞,-2),($\frac{1}{2}$,+∞);
极小值为f(-2)=$\frac{-2+\frac{3}{4}}{1+4}$=-$\frac{1}{4}$;
(2)当a=0时,f(x)=$\frac{x}{1+{x}^{2}}$,当x∈[0,2],f(x)≥0,
且0<x≤2时,x+$\frac{1}{x}$≥2$\sqrt{x•\frac{1}{x}}$=2,当且仅当x=1时,f(x)取得最小值2,
f(x)=$\frac{1}{x+\frac{1}{x}}$≤$\frac{1}{2}$.则f(x)在[0,2]的值域为[0,$\frac{1}{2}$];
g(x)=x3-kx的导数为g′(x)=3x2-k,
g(x)在[1,2]上有极值,可得1<$\sqrt{\frac{k}{3}}$<2,
解得3<k<12,
由g(x)在(1,$\sqrt{\frac{k}{3}}$)递减,在($\sqrt{\frac{k}{3}}$,2)递增,
可得g(x)在[1,2]的最小值为g($\sqrt{\frac{k}{3}}$)=$\frac{k}{3}$$\sqrt{\frac{k}{3}}$-k$\sqrt{\frac{k}{3}}$=-$\frac{2k}{3}$$\sqrt{\frac{k}{3}}$<0,
g(1)=1-k,g(2)=8-2k,
当k=7时,g(1)=g(2)=-6为g(x)的最大值,符合题意;
当k>7时,g(1)>g(2),1-k为g(x)的最大值,
由题意可得1-k<0,即k>1,故k>7成立;
当k<7时,g(1)<g(2),8-2k为g(x)的最大值,
由题意可得8-2k<0,即k>4,故4<k<7成立;
综上可得k的取值范围是(4,12).
点评 本题考查导数的运用:求单调区间和极值、最值,考查不等式恒成立问题的解法,注意运用分类讨论的思想方法,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},\frac{3}{4})$ | B. | $[-\frac{1}{2},\frac{3}{4}]$ | C. | $(-∞,\frac{1}{2}]∪(\frac{3}{4},+∞)$ | D. | $[-\frac{1}{2},\frac{3}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
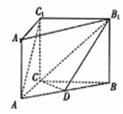 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=2,AC⊥BC,D是线段AB上一点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=2,AC⊥BC,D是线段AB上一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
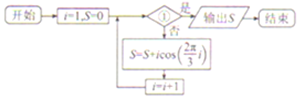
| A. | i>4? | B. | i≥4? | C. | i>3? | D. | i≥3? |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{5}{2}$i | B. | -$\frac{5}{2}$ | C. | $\frac{5}{2}$i | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<2} | B. | {x|x≤2} | C. | {x|2<x≤3} | D. | {x|2≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -4 | C. | $-\frac{3}{4}$ | D. | $-\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com