
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①回归方程$\stackrel{∧}{y}$=2-3x,变量x增加一个单位时,y平均减少3个单位,可判断①错误;
②写出命题p:“?x0∈R,x02-x0-1>0”的否定¬p:“?x∈R,x2-x-1≤0”,可判断②正确;
③由残差平方和越小的模型,拟合的效果越好,可判断③正确;
④用相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$来刻画回归效果,R2的值越大,说明模型的拟合效果越好,可判断④错误.
解答 解:对于①,回归方程$\stackrel{∧}{y}$=2-3x,变量x增加一个单位时,y平均减少3个单位,故①错误;
对于②,命题p:“?x0∈R,x02-x0-1>0”的否定¬p:“?x∈R,x2-x-1≤0”,故②正确;
对于③,残差平方和越小的模型,拟合的效果越好,故③正确;
对于④,用相关指数R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\stackrel{∧}{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$来刻画回归效果,R2越大,说明模型的拟合效果越好,故④不正确.
综上所述,以上命题中正确的有两个,
故选:B.
点评 本题考查命题的真假判断与应用,考查两个变量的线性回归方程及用来描述拟合效果好坏的量,命题及其否定的关系,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
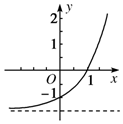 已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,
已知函数f(x)=ax+b(a>0,且a≠1).若f(x)的图象如图所示,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3×223 | B. | 3×224 | C. | 223 | D. | 224 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com