
分析 根据指数幂,对数运算法则和特殊三角函数值可得答案.
解答 解:$\root{5}{2}$×(4${\;}^{-\frac{2}{5}}$)-1+lg$\sqrt{1000}$-sin270°
=${2}^{\frac{1}{5}}$×(${2}^{-\frac{4}{5}}$)-1+lg$100{0}^{\frac{1}{2}}$+1
=${2}^{\frac{1}{5}}$×${2}^{\frac{4}{5}}$+$\frac{3}{2}+1$
=2+$\frac{3}{2}+1$
=$\frac{9}{2}$
故答案为$\frac{9}{2}$
点评 本题考查了指数幂,对数运算法则和特殊三角函数值计算.属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{51}{8}]$ | B. | (-∞,3] | C. | $[\frac{51}{8},+∞)$ | D. | [3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},\frac{3}{4})$ | B. | $[-\frac{1}{2},\frac{3}{4}]$ | C. | $(-∞,\frac{1}{2}]∪(\frac{3}{4},+∞)$ | D. | $[-\frac{1}{2},\frac{3}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 10 | C. | 20 | D. | -20 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
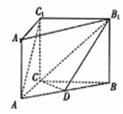 如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=2,AC⊥BC,D是线段AB上一点.
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=2,AC⊥BC,D是线段AB上一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com