
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$或$\frac{5π}{6}$ |
分析 化简求出cosA,得出sinA,利用正弦定理得到sinB,判断B的范围得出B.
解答 解:∵cos(B+C)=-cosA,∴-5cosA+3=0.解得cosA=$\frac{3}{5}$.
∴sinA=$\frac{4}{5}$.
由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{4}{\frac{4}{5}}=\frac{\frac{5}{2}}{sinB}$,解得sinB=$\frac{1}{2}$.
∴B=$\frac{π}{6}$或$\frac{5π}{6}$.
∵sinA=$\frac{4}{5}$$>\frac{1}{2}$,∴A$>\frac{π}{6}$,
∴B<$\frac{5π}{6}$.
∴B=$\frac{π}{6}$.
故选:A.
点评 本题考查了正弦定理得应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
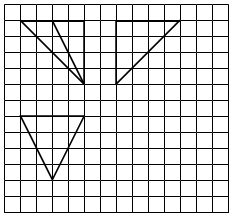
| A. | $\frac{16}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{64}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
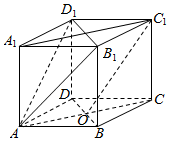 在直平行六面体ABCD-A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1=1.
在直平行六面体ABCD-A1B1C1D1中,底面ABCD是菱形,∠DAB=60°,AC∩BD=O,AB=AA1=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
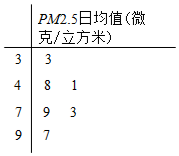 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为1级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为1级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
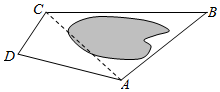 如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为7km.
如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为7km.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com