
已知函数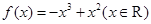 ,
, 满足
满足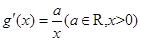 ,且
,且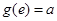 ,
, 为自然对数的底数.
为自然对数的底数.
(1)已知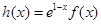 ,求
,求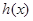 在
在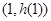 处的切线方程;
处的切线方程;
(2)若存在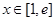 ,使得
,使得
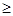
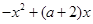 成立,求
成立,求 的取值范围;
的取值范围;
(3)设函数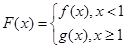 ,
, 为坐标原点,若对于
为坐标原点,若对于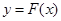 在
在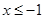 时的图象上的任一点
时的图象上的任一点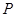 ,在曲线
,在曲线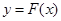
 上总存在一点
上总存在一点 ,使得
,使得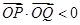 ,且
,且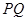 的中点在
的中点在 轴上,求
轴上,求 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:解答题
设函数f(x)=ex-ax-2.
(1)求f(x)的单调区间;
(2)若a=1,k为整数,且当x>0时,(x-k)f′(x)+x+1>0,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某水产养殖场拟造一个无盖的长方体水产养殖网箱,为了避免混养,箱中要安装一些筛网,其平面图如下,如果网箱四周网衣(图中实线部分)建造单价为每米56元,筛网(图中虚线部分)的建造单价为每米48元,网箱底面面积为160平方米,建造单价为每平方米50元,网衣及筛网的厚度忽略不计.
(1)把建造网箱的总造价y(元)表示为网箱的长x(米)的函数,并求出最低造价;
(2)若要求网箱的长不超过15米,宽不超过12米,则当网箱的长和宽各为多少米时,可使总造价最低?(结果精确到0.01米)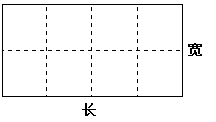
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=lnx-mx(m R).
R).
(1)若曲线y=f(x)过点P(1,-1),求曲线y=f(x)在点P处的切线方程;
(2)求函数f(x)在区间[1,e]上的最大值;
(3)若函数f(x)有两个不同的零点x1,x2,求证:x1x2>e2.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某风景区在一个直径AB为100米的半圆形花园中设计一条观光线路(如图所示).在点A与圆
弧上的一点C之间设计为直线段小路,在路的两侧边缘种植绿化带;从点C到点B设计为沿弧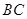 的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
的弧形小路,在路的一侧边缘种植绿化带.(注:小路及绿化带的宽度忽略不计)
(1)设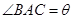 (弧度),将绿化带总长度表示为
(弧度),将绿化带总长度表示为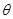 的函数
的函数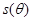 ;
;
(2)试确定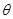 的值,使得绿化带总长度最大.
的值,使得绿化带总长度最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com