
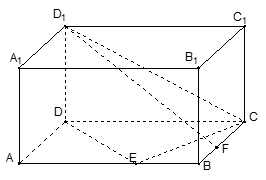
 DE于H,连结C1H
DE于H,连结C1H CC1
CC1 面ABCD,CH为C1H在面ABCD上的射影
面ABCD,CH为C1H在面ABCD上的射影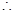 C1H
C1H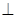 DE
DE 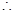
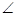 C1HC为二面角C—DE—C1的平面角
C1HC为二面角C—DE—C1的平面角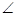 EDC=
EDC= ,
,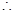
 DCH中得CH=
DCH中得CH= ,
,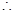
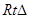 C1HC中,
C1HC中,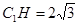 ,
,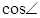 C1HC
C1HC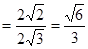
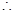 二面角C—DE—C1的余弦值为
二面角C—DE—C1的余弦值为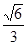 7分
7分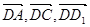 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
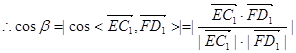
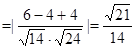
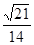 14分
14分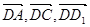 分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)
分别为x轴,y轴,z轴的正向建立空间直角坐标系,则有A(3,0,0)、D1(0,0,2)、B(3,4,0),E(3,3,0)、F(2,4,0)、C1(0,4,2)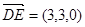 ,
,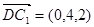 ,
,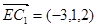
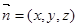 与平面C1DE垂直,则有
与平面C1DE垂直,则有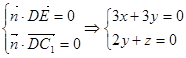 ,
,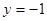 ,则
,则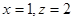
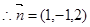
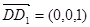
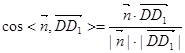
 7分
7分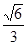 8分
8分
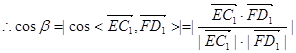
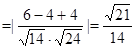
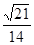 14分
14分

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
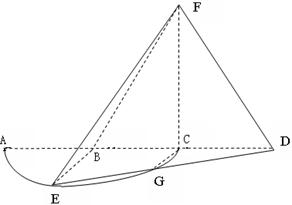
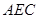 是半径为
是半径为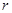 的半圆,
的半圆,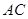 为直径,点
为直径,点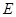 为弧
为弧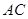 的中点,点
的中点,点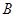 和点
和点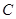 为线段
为线段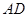 的三等分点,线段
的三等分点,线段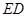 与弧
与弧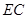 交于点
交于点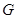 ,且
,且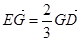 ,平面
,平面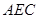 外一点
外一点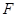 满足
满足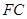
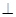 平面
平面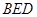 ,
,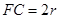 。
。
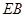
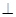
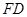 ;
; (及其内部)绕
(及其内部)绕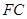 所在直线旋转一周形成一几何体,求该几何体的体积。
所在直线旋转一周形成一几何体,求该几何体的体积。查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
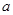 的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=
的正方形E,F分别为PC,BD的中点,侧面PAD⊥底面ABCD,且PA=PD=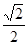 AD.
AD.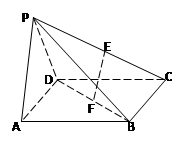
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
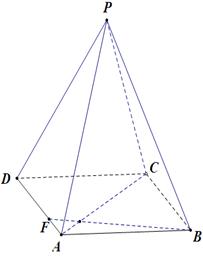
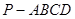 中,AB=1,侧棱
中,AB=1,侧棱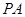 与底面
与底面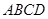 所成角的正切值为
所成角的正切值为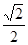 .
.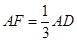 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
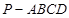 中,平面
中,平面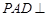 平面
平面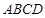 ,平面
,平面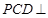 平面
平面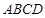 ,
,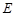 为
为 上任意一点,
上任意一点,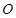 为菱形
为菱形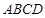 对角线的交点.
对角线的交点.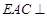 平面
平面 ;
;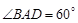 ,三棱锥
,三棱锥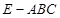 的体积是四棱锥
的体积是四棱锥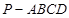 的体积的
的体积的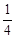 ,二面角
,二面角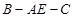 的大小为
的大小为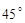 ,求
,求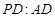

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com