Question

15．为了测量学校操场四边形ABCD的周长和面积，在操场中间取一点O．测得OA=40m，OB=37m，OC=42m，OD=44m，且∠DOA=120°，∠AOB=60°，∠BOC=45°，∠COD=135°．
（1）试求四边形的周长；
（2）试求四边形的面积．

Answer 1

分析 （1）使用余弦定理求出操场的边长；
（2）分别求出4个小三角形的面积．

解答 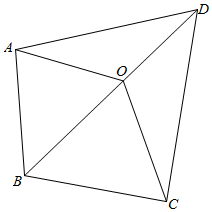解：（1）在△AOB中，由余弦定理得：
AB²=OA²+OB²-2OA•OBcos∠AOB=1489，∴AB≈38.6m．
同理可得BC²=OB²+OC²-2OB•OCcos∠BOC=935.3，∴BC≈30.9m
CD²=OD²+OC²-2OD•OCcos∠DOC=6313.47，∴BC≈79.5m
AD²=OA²+OD²-2OA•ODcos∠AOD=5296，∴BC≈72.77m
∴AB+BC+CD+AD=38.6+30.9+79.5+72.77=221.4m
即四边形的周长为221.4m．
（2）S_△AOB=$\frac{1}{2}OA×OBsin∠AOB$=370$\sqrt{3}$，
S_△BOC=$\frac{1}{2}OB×OC×sin∠BOC$=$\frac{777\sqrt{2}}{2}$，
S_△COD=$\frac{1}{2}×OC×OD×sin∠COD$=462$\sqrt{2}$，
S_△AOD=$\frac{1}{2}×OA×OD×sin∠AOD$=440$\sqrt{3}$．
∴四边形的面积S=S_△AOB+S_△BOC+S_△COD+S_△AOD=810$\sqrt{3}$+$\frac{1701\sqrt{2}}{2}$．

点评 本题考查了余弦定理的应用，三角形的面积公式，属于中档题．