
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 利用三角函数的最值,求出自变量x1,x2的值,然后判断选项即可.
解答 解:将函数f(x)=sin2x的图象向右平移$φ({0<φ<\frac{π}{2}})$个单位后得到函数g(x)=sin(2x-2φ)的图象,
若对满足|f(x1)-g(x2)|=2的x1,x2,有$|{{x_1}-{x_2}}|=\frac{π}{6}$,
故两个函数的最大值与最小值的差为2,有|x1-x2|min=$\frac{π}{6}$,
不妨设x1=$\frac{π}{4}$,x2=$\frac{5π}{12}$,则g(x2)=sin(2x2-2φ)=sin($\frac{5π}{6}$-2φ)=-1,
则φ的最小正值为$\frac{π}{6}$,检验满足条件,
故选:D.
点评 本题考查三角函数的图象平移,函数的最值以及函数的周期的应用,考查分析问题解决问题的能力,是好题,题目新颖.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | -$\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=2,n=2,依次输入的a为3,3,7,则输出的s=( )| A. | 9 | B. | 21 | C. | 25 | D. | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
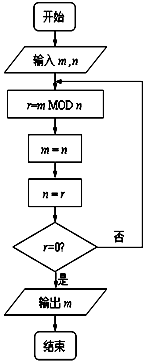 如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMOD n”表示m除以n的余数),若输入的m,n分别为72,15,则输出的m=( )
如图程序框图的算法思路源于数学名著《几何原本》中的“辗转相除法”,执行该程序框图(图中“mMOD n”表示m除以n的余数),若输入的m,n分别为72,15,则输出的m=( )| A. | 12 | B. | 3 | C. | 15 | D. | 45 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com