
| A. | $\sqrt{2}$ | B. | 5 | C. | 2 | D. | $\sqrt{5}$ |
分析 由双曲线方程求得双曲线的一条渐近线方程,与抛物线方程联立消去y,进而根据判别式等于0求得b=a,进而根据c=$\sqrt{{a}^{2}+{b}^{2}}$,求得e=$\frac{c}{a}$即离心率.
解答 解:双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线为y=$\frac{b}{a}$x,
由方程组$\left\{\begin{array}{l}{y=\frac{b}{a}x}\\{y=\frac{1}{2}{x}^{2}+\frac{1}{2}}\end{array}\right.$,消去y,
$\frac{1}{2}$x2-$\frac{b}{a}$x+$\frac{1}{2}$=0有唯一解,
所以△=($\frac{b}{a}$)2-4×$\frac{1}{2}$×$\frac{1}{2}$=0,
所以b=a,
e=$\frac{c}{a}$=$\sqrt{1+(\frac{b}{a})^{2}}$=$\sqrt{2}$.
故选:A.
点评 本题主要考查了双曲线的简单性质.离心率问题是圆锥曲线中常考的题目,解决本题的关键是找到a和b或a和c或b和c的关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $4\sqrt{3}$ | B. | 4 | C. | -4$\sqrt{3}$ | D. | -4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 推理形式错误 | B. | 大前提错误 | ||
| C. | 小前提错误 | D. | 大前提和小前提都错误 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2017}{2}$ | B. | 2017 | C. | $\frac{2018}{2}$ | D. | 2018 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
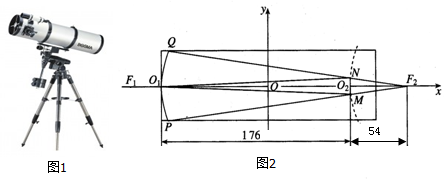
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com