
分析 (1)由题意可得k=f(x)=$\frac{1+lnx}{x}$(x>0),求出导数,求得单调区间,可得极值点,再由0<m<1<m+$\frac{1}{2}$,解不等式可得所求范围;
(2)运用参数分离可得$t≥\frac{(x+1)(1+lnx)}{x}$,令$g(x)=\frac{(x+1)(1+lnx)}{x}(x≥1)$,求出导数,再令h(x)=x-lnx(x≥1),求出导数,判断单调性,即可得到g(x)的单调性,可得g(x)≥g(1)=2,由t大于等于最小值即可.
解答 解:(1)由题意可得k=f(x)=$\frac{1+lnx}{x}$(x>0),
即有f′(x)=-$\frac{lnx}{{x}^{2}}$,
当0<x<1时,f'(x)>0;当x>1时,f'(x)<0,
可得f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,
故f(x)在x=1处取得极大值,
由函数f(x)在区间$(m,m+\frac{1}{2})(m>0)$上存在极值,
可得$\left\{\begin{array}{l}0<m<1\\ m+\frac{1}{2}>1\end{array}\right.$,得$\frac{1}{2}<m<1$,
即实数m的取值范围是$(\frac{1}{2},1)$;
(2)由题意$f(x)≤\frac{t}{x+1}$,得$t≥\frac{(x+1)(1+lnx)}{x}$,
令$g(x)=\frac{(x+1)(1+lnx)}{x}(x≥1)$,
则$g'(x)=\frac{x-lnx}{x^2}(x≥1)$,
令h(x)=x-lnx(x≥1),
则$h'(x)=1-\frac{1}{x}=\frac{x-1}{x}$,
由x≥1,可得h'(x)≥0,
故h(x)在[1,+∞)上单调递增,
则h(x)≥h(1)=1>0,从而g'(x)>0,
故g(x)在[1,+∞)上单调递增,
则g(x)≥g(1)=2,
故实数t的取值范围是[2,+∞).
点评 本题考查导数的运用:求单调区间和极值、最值,考查存在性问题的解法,注意运用参数分离和构造函数,通过导数判断单调性,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
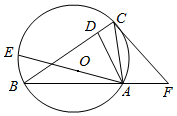 如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.
如图,AE是⊙O的直径,△ABC内接于⊙O,AB=BC,AD⊥BC,垂足为D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com