
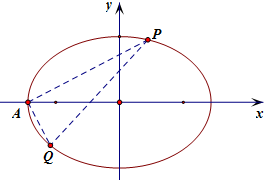
 如图,已知抛物线y=ax2(a>0).过焦点F的直线与此抛物线交于A(x1,y1),B(x2,y2)两点,设M是点B在y轴上的射影,准线l与y轴交于点N
如图,已知抛物线y=ax2(a>0).过焦点F的直线与此抛物线交于A(x1,y1),B(x2,y2)两点,设M是点B在y轴上的射影,准线l与y轴交于点N分析 (1)求得抛物线的焦点和准线方程,设直线AB的方程是:x=m(y-$\frac{1}{4a}$),代入抛物线方程,运用韦达定理,即可得证;
(2)①若AB⊥AN,则AO=ON,由两点的距离公式,结合抛物线方程和(1)的结论,化简即可得证;
②求得M的坐标,运用两点的距离公式求得MA,MB,化简整理,结合前面的结论,即可得到MA=MB,进而得证.
解答 证明:(1)抛物线y=ax2(a>0)的焦点为(0,$\frac{1}{4a}$),准线为y=-$\frac{1}{4a}$.
设直线AB的方程是:x=m(y-$\frac{1}{4a}$),
代入y=ax2整理得:am2y2-$\frac{{m}^{2}+2}{2}$y+$\frac{{m}^{2}}{16a}$=0,
利用韦达定理,可得y1y2=$\frac{1}{16{a}^{2}}$;
(2)①若AB⊥AN,则AO=ON,
即有$\sqrt{{{x}_{1}}^{2}+{{y}_{1}}^{2}}$=$\frac{1}{4a}$,
由y1=ax12,可得
y12+$\frac{{y}_{1}}{a}$=$\frac{1}{16{a}^{2}}$,
即有1-16a2y12=16ay1,
则y2-y1=$\frac{1}{16{a}^{2}{y}_{1}}$-y1=$\frac{1-16{a}^{2}{{y}_{1}}^{2}}{16{a}^{2}{y}_{1}}$=$\frac{16a{y}_{1}}{16{a}^{2}{y}_{1}}$=$\frac{1}{a}$;
②M(0,y2),
MA=$\sqrt{{{x}_{1}}^{2}+({y}_{1}-{y}_{2})^{2}}$=$\sqrt{{{x}_{1}}^{2}+\frac{1}{{a}^{2}}}$,
MB=$\sqrt{{{x}_{2}}^{2}}$,
由于y2-y1=ax22-ax12=$\frac{1}{a}$,
即有x22=x12+$\frac{1}{{a}^{2}}$.
则MA=MB,
则△MAB为等腰三角形,
即有∠MAB=∠MBA.
点评 本题考查抛物线的方程和性质,主要考查抛物线的方程和直线方程联立,运用韦达定理,同时考查两点的距离公式的运用,属于中档题.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{5}$ | B. | $\frac{5}{7}$ | C. | $\frac{7}{12}$ | D. | $\frac{5}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,一个直径AB=2的半圆,过点A作这个圆所在平面的垂线,在垂线上取一点S,使AS=AB,C为半圆上的一个动点,M、N分别在SB、SC上,且AN⊥SC,AM⊥SB.
如图所示,一个直径AB=2的半圆,过点A作这个圆所在平面的垂线,在垂线上取一点S,使AS=AB,C为半圆上的一个动点,M、N分别在SB、SC上,且AN⊥SC,AM⊥SB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{ln2}$+$\frac{3(lo{g}_{2}3)}{ln2}$-1 | B. | 3log2$\frac{3}{ln2}$-$\frac{3}{ln2}$-1 | ||
| C. | log23-3log2$\frac{3}{ln2}$+1 | D. | $\frac{3}{ln2}$-$\frac{3(lo{g}_{2}3)}{ln2}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com