Question

17．已知椭圆C的中心为坐标原点，长轴长为4，一条准线方程为x=-4

（1）求椭圆C的标准方程；
（2）求椭圆C被直线y=x+1截得的弦长；
（3）已知点A为椭圆的左顶点，过点A作斜率为k₁，k₂的两条直线与椭圆分别交于点P，Q，若k₁•k₂=-1，证明：直线PQ过定点，并求出定点的坐标．

Answer 1

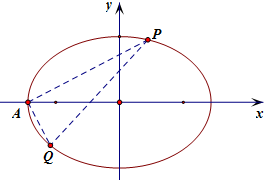
分析 （1）由条件利用椭圆的定义、性质，求出a、b的值，可得椭圆C的标准方程．
（2）把y=x+1代入椭圆C的标准方程，利用韦达定理、弦长公式求得椭圆C被直线y=x+1截得的弦长．
（3）设出PA的方程，并把它代入椭圆的方程，求得P、Q的坐标，可得PQ的斜率，可得直线PQ的方程，从而得到直线PQ经过定点．

解答 解：（1）由题意可得2a=4，$\frac{{a}^{2}}{c}$=4，∴a=2，c=1，∴b²=a²-c²=3，
∴椭圆C的标准方程为 $\frac{x^2}{4}+\frac{y^2}{3}=1$．
（2）把y=x+1代入椭圆C的标准方程 $\frac{x^2}{4}+\frac{y^2}{3}=1$，可得7x²+8x-8=0，
∴x₁+x₂=-$\frac{8}{7}$，x₁•x₂=-$\frac{8}{7}$，
故弦长为$\sqrt{{1+k}^{2}}$|x₁-x₂|=$\sqrt{2}$•$\sqrt{{{（x}_{1}{+x}_{2}）}^{2}-{4x}_{1}{•x}_{2}}$=$\sqrt{2}$•$\sqrt{\frac{64}{49}+\frac{4×8}{7}}$=$\sqrt{2}$•$\frac{12\sqrt{2}}{7}$=$\frac{24}{7}$．
（3）由题意可得A（-2，0），设直线PA斜率为k，∴PA方程为y=k（x+2），
代入椭圆方程可得 （3+4k²）x²+16k²x+16k²-12=0，求得：x=$\frac{6-{8k}^{2}}{3+{4k}^{2}}$，或 x=$\frac{{6k}^{2}-8}{3{+4k}^{2}}$，
可得  $P（\frac{{6-8{k^2}}}{{3+4{k^2}}}，\frac{12k}{{3+4{k^2}}}）$，$Q（\frac{{6{k^2}-8}}{{4+3{k^2}}}，\frac{-12k}{{4+3{k^2}}}）$．
当k≠±1时，求得PQ的斜率 ${k_{PQ}}=\frac{7k}{{4（1-{k^2}）}}$，
可得PQ方程为$y-\frac{12k}{{3+4{k^2}}}=\frac{7k}{{4（1-{k^2}）}}（x-\frac{{6-8{k^2}}}{{3+4{k^2}}}）$，令y=0，求得x=-$\frac{2}{7}$，故当k≠±1时，直线PQ经过点（-$\frac{2}{7}$，0），
综上可得，直线PQ经过点（-$\frac{2}{7}$，0）．

点评 本题主要考查椭圆的定义、性质和标准方程，直线和圆锥曲线的位置关系，弦长公式的应用，考查计算能力，体现了转化、分类讨论的数学思想，属于难题．