
| A. | 3 | B. | -6 | C. | 2 | D. | 1 |
分析 a1=2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N*),可得:an+4=an.即可得出.
解答 解:∵a1=2,an+1=$\frac{1+{a}_{n}}{1-{a}_{n}}$(n∈N*),
∴a2=$\frac{1+2}{1-2}$=-3,同理可得:a3=-$\frac{1}{2}$,a4=$\frac{1}{3}$,a5=2,a6=-3,…,
可得:an+4=an.
则该数列的前2014项的乘积=$({a}_{1}{a}_{2}{a}_{3}{a}_{4})^{503}$×a1a2=$[2×(-3)×(-\frac{1}{2})×\frac{1}{3}]^{503}$×2×(-3)=-6.
故选:B.
点评 本题考查了数列递推关系、数列通项公式、数列的周期性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
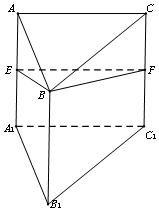 三棱柱ABC-A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=$\sqrt{2}$,∠A1AB=45°,E、F分别为AA1、CC1的中点.
三棱柱ABC-A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=$\sqrt{2}$,∠A1AB=45°,E、F分别为AA1、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (8,24) | B. | (10,18) | C. | (12,18) | D. | (12,15) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com