
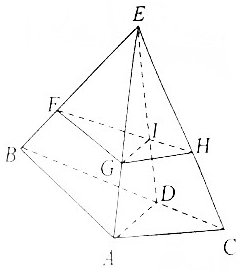
 在三棱锥E-ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC,F,G,H是EB,EA,EC上的点,FH与ED交于点I.
在三棱锥E-ABC中,AB⊥AC,AB=1,AC=$\frac{\sqrt{2}}{2}$,点D在线段BC上,且BD=2CD,ED⊥平面ABC,F,G,H是EB,EA,EC上的点,FH与ED交于点I.分析 (I)由题意可证FG∥BA,FH∥BC,进而可证平面FGH∥平面ABC,利用面面平行的性质即可证明GI∥AD;
(Ⅱ)由已知可求BC,BD,DC的值,由于cos2B+cos2C=1,设AD=x,则由余弦定理可得27x4-42x2+11=0,解得AD,利用勾股定理可求AD⊥BC,利用线面垂直的性质可证ED⊥AD,进而可证AD⊥平面EBD,利用线面垂直的性质可证AD⊥BE.
解答 证明:(I)∵由题意,$\frac{EF}{EB}$=$\frac{EG}{EA}$=$\frac{EH}{EC}$=$\frac{2}{3}$,则FG∥BA,FH∥BC,
又∵AB∩BD=B,FG∩FH=F,
∴平面FGH∥平面ABC,
∵平面EAD∩平面ABC=AD,平面EAD∩平面FGH=GI,
∴GI∥AD;
(Ⅱ)∵AB=1,AC=$\frac{\sqrt{2}}{2}$,AB⊥AC,
∴BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\frac{\sqrt{6}}{2}$,
∵BD=2CD,可得:BD=$\frac{\sqrt{6}}{3}$,DC=$\frac{\sqrt{6}}{6}$,
∴由cos2B+sin2B=1,cos2B+cos2C=1,
∴设AD=x,则由余弦定理可得:[$\frac{1+(\frac{\sqrt{6}}{3})^{2}-{x}^{2}}{2×\frac{\sqrt{6}}{3}}$]2+[$\frac{(\frac{\sqrt{6}}{6})^{2}+(\frac{\sqrt{2}}{2})^{2}-{x}^{2}}{2×\frac{\sqrt{6}}{6}×\frac{\sqrt{2}}{2}}$]2=1,
整理可得:27x4-42x2+11=0,解得:x=$\frac{\sqrt{3}}{3}$,或$\frac{\sqrt{11}}{3}$(此时,AD>AB>BD,而B为锐角,故舍去),
∴AD=$\frac{\sqrt{3}}{3}$,可得:AD2+BD2=AB2,
∴AD⊥BC,
又∵ED⊥平面ABC,AD?平面ABC,可得:ED⊥AD,且ED∩BC=D,
∴AD⊥平面EBD,
∵BE?平面EBD,
∴AD⊥BE.
点评 本题主要考查了面面平行的性质,余弦定理,勾股定理,线面垂直的判定和性质的综合应用,考查了空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 定义域是$\{x|x≠kπ+\frac{π}{6},(k∈Z)\}$ | B. | 值域是R | ||
| C. | 在其定义域上是增函数 | D. | 最小正周期是π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}$ | B. | $\frac{5}{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6π}}{6}$ | B. | $\frac{\sqrt{π}}{2}$ | C. | $\frac{\sqrt{2π}}{2}$ | D. | $\frac{3\sqrt{π}}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\overrightarrow{a}$+3$\overrightarrow{b}$ | B. | $\overrightarrow{a}$-3$\overrightarrow{b}$ | C. | 3$\overrightarrow{a}$-$\overrightarrow{b}$ | D. | -3$\overrightarrow{a}$+$\overrightarrow{b}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com