练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知命题p：“?x∈[1,2]，x2－a≥0”；命题q：“?x∈R，x2＋2ax＋2－a＝0”．若命题“p且q”是真命题，则实数a的取值范围为(　　)

    A．a≤－2或a＝1

    B．a≤－2或1≤a≤2

    C．a≥1

    D．－2≤a≤1

     

    A

    【解析】

    由已知可知p和q均为真命题.

    若x∈[1,2],则x2∈[1,4],

    由x2－a≥0a≤x2∴命题p为真得a≤1，

    又命题q为真得,所以△=4a2-4(2-a)≥0,即a≤－2或a≥1，

    综合得a≤－2或a＝1.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014高考名师推荐数学理科参数方程（解析版） 题型：填空题

    如图,以过原点的直线的倾斜角为参数,则圆的参数方程为 .

     

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科函数与方程（解析版） 题型：填空题

    已知函数，若函数有两个不同的零点，则实数k的取值范围是 。

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科几何概型（解析版） 题型：选择题

    在长为12cm的线段AB上任取一点C．现作一矩形，邻边长分别等于线段AC，CB的长，则该矩形面积小于32cm2的概率为（ ）

    A． B． C． D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科全称量词与存在性量词（解析版） 题型：选择题

    已知命题p：?x0∈R，使sin x0＝；命题q：?x∈R，都有x2＋x＋1＞0.

    给出下列结论 ①命题“p∧q”是真命题； ②命题“?p∨?q”是假命题；

    ③命题“?p∨q”是真命题； ④命题“p∨?q”是假命题．

    其中正确的是

    A．②③

    B．②④

    C．③④

    D．①②③

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科余弦定理（解析版） 题型：选择题

    已知A，B，C为△ABC的三个内角，其所对的边分别为a，b，c，若A=，a＝2，b＋c＝4，则△ABC的面积为(    )

    A．2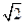

    B．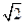

    C．3

    D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科二项式定理与性质（解析版） 题型：填空题

    在的展开式中，x3的系数是_____（结果用数值表示）．

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学理科两角和与差的三角函数、倍角公式（解析版） 题型：选择题

    设函数f(x)=sin(x+)+cos(x+)(>0,||<)的最小正周期为π，且f(-x)=f(x),则（ ）

    A.y=f(x) 在(0,)单调递减

    B. y=f(x)在(,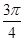)单调递减

    C. y=f(x)在(0,)单调递增

    D. y=f(x)在(,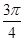)单调递增

     

    查看答案和解析>>

    科目：高中数学 来源：2014高考名师推荐数学文科预测题（解析版） 题型：解答题

    设函数。

    （1）若，求的单调区间；

    （2）若当时，，求a的取值范围。

     

    查看答案和解析>>

    同步练习册答案