
分析 根据对称关系得出t=1,根据命题为真求出m的范围,根据f(x)的函数图象判断出零点个数.
解答 解:∵f(x)的图象关于x=-$\frac{1}{2}$对称,且f(0)=0,
∴f(-1)=0,即|-1+t|=0,解得t=1.
∴f(x)=$\left\{\begin{array}{l}{|x+1|,x≤-\frac{1}{2}}\\{|x|,x>-\frac{1}{2}}\end{array}\right.$,
∵对?x∈[1,+∞),ex>2mex是真命题,∴m<$\frac{{e}^{x}}{2ex}$恒成立,x∈[1,+∞).
令h(x)=$\frac{{e}^{x}}{2ex}$,则h′(x)=$\frac{{e}^{x}•2ex-{e}^{x}•2e}{4{e}^{2}{x}^{2}}$=$\frac{2{e}^{x+1}(x-1)}{4{e}^{2}{x}^{2}}$≥0,
∴h(x)在[1,+∞)上单调递增,
∴hmin(x)=h(1)=$\frac{1}{2}$,
∴0<m$<\frac{1}{2}$.
作出f(x)的函数图象如图所示: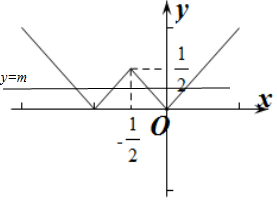
由图象可知y=f(x)与y=m有4个交点,
∴g(x)=f(x)-m有4个零点.
故答案为:4.
点评 本题考查了函数恒成立问题与函数最值计算,函数零点个数与函数图象的关系,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{32}{3}$π | C. | $\frac{8}{3}$π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| PM2.5 | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
| 空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 重度污染 | 中重度污染 | 重度污染 |
| 天数 | 4 | 15 | 18 | 30 | 7 | 11 | 15 |
| P(k2≥k0) | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 1.32 | 2.07 | 2.70 | 3.841 | 5.02 | 6.63 | 7.87 | 10.828 |
| 非重度污染 | 重度污染 | 合计 | |
| 供暖季 | |||
| 非供暖季 | |||
| 合计 | 100 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com