Question

2．将函数y=sin（ωx-$\frac{π}{6}$）（ω＞0）的图象向左平移$\frac{π}{3ω}$个单位，得到函数f（x）的图象，若函数f（x）在（0，2]上恰有一个最大值1和最小值-1，则ω的取值范围是$\frac{2π}{3}$≤ω＜$\frac{7π}{6}$．

Answer 1

分析 根据三角函数的图象变换关系，先求出函数f（x）的解析式，然后求出ωx+$\frac{π}{6}$的取值范围，利用数形结合进行求解即可．

解答 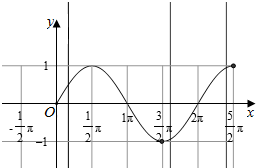解：y=sin（ωx-$\frac{π}{6}$）（ω＞0）的图象向左平移$\frac{π}{3ω}$个单位，
得到y=sin[ω（x+$\frac{π}{3ω}$）-$\frac{π}{6}$]=sin（ωx+$\frac{π}{6}$），
即f（x）=sin（ωx+$\frac{π}{6}$），
当0＜x≤2时，$\frac{π}{6}$＜ωx+$\frac{π}{6}$≤2ω+$\frac{π}{6}$，
要使函数f（x）在（0，2]上恰有一个最大值1和最小值-1，
则$\frac{3π}{2}$≤2ω+$\frac{π}{6}$＜$\frac{5π}{2}$，
即$\frac{8π}{6}$≤2ω＜$\frac{14π}{6}$，
即即$\frac{2π}{3}$≤ω＜$\frac{7π}{6}$，
故答案为：$\frac{2π}{3}$≤ω＜$\frac{7π}{6}$．

点评 本题主要考查三角函数的图象和性质，根据条件求出函数的解析式，利用三角函数的图象和性质建立不等式关系是解决本题的关键．综合性较强．