
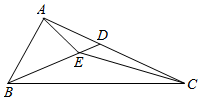
 已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.
已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.分析 (1)根据图象和已知的角求出∠ADB,在△ABD中由正弦定理求出AD的长;
(2)根据题意在∠BAC的平分线上截取AO=AC,连接OA、OB、OC、OE,OA交BC于点F,根据图形和已知角的度数、三角形全等定理证明△ABO≌△AFC,由角的关系和外接圆的性质证明△OCE为正三角形,可得EO=EC,由三角形全等定理证明△AEO≌△AEC,得到∠OAE=20°,即可证明结论.
解答 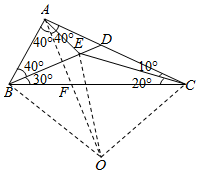 解:(1)∵∠DCE=10°,∠ECB=20°,∴∠DCB=30°,
解:(1)∵∠DCE=10°,∠ECB=20°,∴∠DCB=30°,
∵∠DBC=30°,∴∠ADB=∠DBC+∠BCD=60°,
在△ABD中,∠DBA=40°,AB=$\frac{2}{sin40°}$,
由正弦定理得$\frac{AD}{sin∠ABD}=\frac{AB}{sin∠ADB}$,
AD=$\frac{AB•sin∠ABD}{sin∠ADB}$=$\frac{\frac{2}{sin40°}•sin40°}{sin60°}$=$\frac{4\sqrt{3}}{3}$;
证明:(2)在∠BAC的平分线上截取AO=AC
连接OA、OB、OC、OE,OA交BC于点F.
①证△ABO≌△AFC(SAS),BO=CO
∵∠BAF=40°,∠ABF=70°,
∴∠AFB=70°,则AB=AF;
∵∠BAO=40°=∠FAC;AO=AC;
∴△ABO≌△AFC(SAS),∴BO=FC.∵AO=AC,∠OAC=40°,∴∠AOC=∠ACO=70°,
又∵∠CFO=∠ABF=70°,
∴∠AOC=∠CFO,FC=OC,∴BO=CO;
②证△COE为正三角形,EO=EC,
∵∠OCB=∠ACO-∠ACB=70°-30°=40°,∠OBC=40°,∴∠BOC=100°.
∵∠BEC=180°-30°-20°=130°.∴∠BEC+$\frac{1}{2}$∠BOC=180°,BO=CO,
∴O在BC的中垂线上,O为△EBC外接圆的圆心,∠BOC为圆心角.
∴OE=OC,
∵∠OCE=∠OCB+∠ECB=40°+20°=60°,∴
△OCE为正三角形,EO=EC;
③证△AEO≌△AEC,∠OAE=20°∵
AO=AC,AE=AE,EO=EC,∴△AEO≌△AEC(SSS).
∴∠OAE=∠CAE=$\frac{1}{2}$×40°=20°,
∴∠BAE=∠BAO+∠OAE=40°+20°=60°.
点评 本题考查了正弦定理,三角形中角之间的关系,以及三角形全等定理的应用,作出辅助线是解题的关键,考查数形结合思想,推理论证能力.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,0) | B. | (1,1) | C. | (cos37°,sin37°) | D. | $\frac{\overline a}{{|{\overline a}|}}(|{\overline a}|≠0)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com