
分析 f(x)=$\sqrt{{x^2}+4x+20}$+$\sqrt{{x^2}+2x+10}$=$\sqrt{(x+2)^{2}+(0-4)^{2}}+\sqrt{(x+1)^{2}+(0+3)^{2}}$,表示平面上点M(x,0)与点N(-2,4),O(-1,-3)的距离和,利用两点间的距离公式,即可得出结论.
解答 解:f(x)=$\sqrt{{x^2}+4x+20}$+$\sqrt{{x^2}+2x+10}$=$\sqrt{(x+2)^{2}+(0-4)^{2}}+\sqrt{(x+1)^{2}+(0+3)^{2}}$,表示平面上点M(x,0)与点N(-2,4),O(-1,-3)的距离和,
∴f(x)=$\sqrt{{x^2}+4x+20}$+$\sqrt{{x^2}+2x+10}$的最小值为$\sqrt{(-2+1)^{2}+(4+3)^{2}}$=5$\sqrt{2}$.
故答案为:5$\sqrt{2}$.
点评 本题考查两点间的距离公式,考查学生分析解决问题的能力,正确转化是关键.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
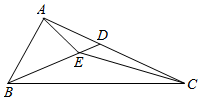 已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.
已知△ABC,点E是三角形内一点,BE延长后交AC于点D,设∠DBC=30°,∠DCE=10°,∠ECB=20°,∠DBA=40°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{16}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | $\frac{16}{3}$ | C. | $\frac{13}{3}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com